
Читайте также:
|
Рассмотрим шарнирно опертую балку с пролетом l с постоянным поперечным сечением с установленной на ней электромотором весом Q с неуравновешенной массой me и эксцентриситетом e. Число оборотов электромотора n об/мин. Будем исследовать напряженно-деформированное состояние в двух случаях: 1) правая опора абсолютно жесткая; 2) правая опора упругая.
Сначала рассмотрим первый случай.
Считаем, что масса электромотора значительно больше всей массы балки. Это позволяет упростить задачу, и пренебречь массой балки по сравнению с массой M электромотора, которую условно считаем приложенной в точке оси балки на расстоянии а от левой опоры (рис. 15.29, а). Для выяснения характера воздействия на балку вращающихся неуравновешенных частей рассмотрим рис.15.30.
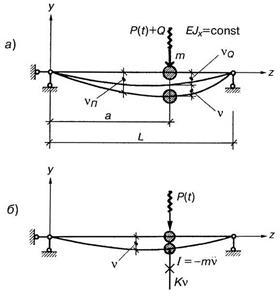
Рис. 15.29
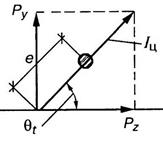
Рис. 15.30
На балку со стороны вращающейся массы me действует центробежная сила
 (15.16)
(15.16)
где V – линейная скорость массы окружности радиуса е. Вычисляем угловую скорость вращения ротора по формуле
 (15.17)
(15.17)
и линейную скорость
 (15.18)
(15.18)
вместо (15.16), получим
 (15.19)
(15.19)
Выразив массу  через вес
через вес  , вместо (15.19) получим
, вместо (15.19) получим
 . (15.20)
. (15.20)
Разложим эту силу на составляющие по осям Y и Z.
 (15.21)
(15.21)
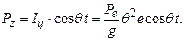 (15.22)
(15.22)
Сила  вызывает изгиб балки, а продольная сила
вызывает изгиб балки, а продольная сила  вызывает деформации растяжения-сжатия, которые в дальнейшем учитывать не будем.
вызывает деформации растяжения-сжатия, которые в дальнейшем учитывать не будем.
Положение массы на плоскости  будет определяться одним параметром – прогибом
будет определяться одним параметром – прогибом  , который можно считать суммой прогибов балки при статическом действии веса неработающего мотора
, который можно считать суммой прогибов балки при статическом действии веса неработающего мотора  и прогиба балки от действия вращающейся неуравновешенной массы
и прогиба балки от действия вращающейся неуравновешенной массы 
 . (15.23)
. (15.23)
Запишем, используя принцип Даламбера, динамическое равновесие массы 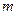 , на которую в произвольный момент времени действует сила инерции, сумма сил
, на которую в произвольный момент времени действует сила инерции, сумма сил  и упругая сила отпора балки при перемещении
и упругая сила отпора балки при перемещении 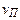 , равная
, равная  , где
, где 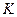 - коэффициент жесткости балки в точке прикрепления мотора. Эта величина численно равна силе, приложенной к балке в этой точке и вызывающей прогиб равный единице. Можно приложить силу
- коэффициент жесткости балки в точке прикрепления мотора. Эта величина численно равна силе, приложенной к балке в этой точке и вызывающей прогиб равный единице. Можно приложить силу  и определить от нее прогиб
и определить от нее прогиб  (рис. 15.31). Тогда
(рис. 15.31). Тогда
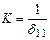 (15.24)
(15.24)
Итак
 (15.25)
(15.25)

Рис. 15.31
Продифференцировав (15.23) дважды по времени, и учтя, что 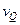 - прогиб не зависит от времени, получим
- прогиб не зависит от времени, получим
 . (15.26)
. (15.26)
Теперь вместо (15.25), получим
 (15.27)
(15.27)
Далее учтем, что по закону Гука
 . (15.28)
. (15.28)
Поэтому вместо (15.26) будем рассматривать дифференциальное уравнение для динамической части прогиба  (рис.15.29,б)
(рис.15.29,б)
 (15.29)
(15.29)
или
 (15.30)
(15.30)
Обозначим 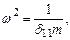 (15.31)
(15.31)
тогда получим дифференциальное уравнение динамического прогиба балки как системы с одной степенью свободы без учета сил сопротивления
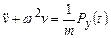 (15.32)
(15.32)
Это дифференциальное уравнение линейное второго порядка с известной правой частью.
В математике доказывается, что решение такого уравнения ищется в виде суммы общего решения однородного дифференциального уравнения
 (15.33)
(15.33)
и частного решения уравнения (15.32).
Однородное дифференциальное уравнение (15.33) описывает свободные или собственные колебания упругой системы с одной степенью свободы.
Свободные колебания вызываются начальными воздействиями. Например, можно медленно отодвинуть массу от положения равновесия и затем отпустить. При этом начальные условия будут иметь вид
 (15.34)
(15.34)
Можно поступить иначе – толкнуть массу. При этом массе сообщается начальная скорость V 0 и начальные условия будут иметь вид
 (15.35)
(15.35)
Известно, что решение уравнения (15.33) можно рассматривать в двух формах
 (15.36)
(15.36)
или
 (15.37)
(15.37)
В той и другой форме участвуют две постоянные интегрирования (А и В) или  , которые можно определить из начальных условий (15.34) или (15.35) или их комбинаций.
, которые можно определить из начальных условий (15.34) или (15.35) или их комбинаций.
Таким образом, собственные колебания (15.37) совершаются по закону синусоиды с амплитудой А 1 и круговой частотой
 (15.38)
(15.38)
Известно, что функции в выражении (15.36) имеют общий период 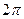 .
.

Отсюда,
 (15.39)
(15.39)
 (15.40)
(15.40)
Таким образом, круговая частота собственных колебаний есть число циклов колебаний за 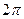 секунд.
секунд.
Коэффициент А 1 характеризует размер колебаний и носит название амплитуды колебания, 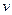 - начальная фаза колебаний.
- начальная фаза колебаний.
Найдем частное решение (15.32), учтя, что функция 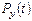 имеет вид (15.21).
имеет вид (15.21).
Обозначим амплитуду возмущающей силы
 (15.41)
(15.41)
Ищем частные решения уравнения
 (15.42)
(15.42)
в виде  (15.43)
(15.43)
Найдем производные по времени
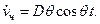 (15.44)
(15.44)
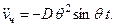 (15.45)
(15.45)
и подставим (15.43), (15.44), (15.45) в (15.42)

откуда 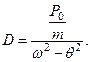 (15.46)
(15.46)
Преобразуем
 ,
,
Учитывая (15.31), получим
 (15.47)
(15.47)
где  - величина прогиба балки от силы
- величина прогиба балки от силы 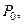 приложенной статическим образом.
приложенной статическим образом.
Итак, частное решение (15.42) имеет вид
 . (15.48)
. (15.48)
Таким образом, выражение динамического прогиба баки как системы с одной степенью свободы без учета сил сопротивления будет
 (15.49)
(15.49)
В предыдущих рассуждениях мы не учли силы сопротивления, которые всегда возникают при колебаниях механических систем. Экспериментально доказано, что они вызывают затухание во времени собственных колебаний. Если все время действует вынуждающая сила, то изменение динамического прогиба при большом t описывается вторым слагаемым в (15.49), которое назовем вынужденным колебанием
 . (15.50)
. (15.50)
Максимальный динамический прогиб будет при
 . (15.51)
. (15.51)
Обозначив
 (15.52)
(15.52)
как коэффициент нарастания колебаний, получим
 (15.53)
(15.53)
Полный максимальный прогиб (15.23) (с учетом постоянно действующего веса электромотора) будет
 (15.54)
(15.54)
где  - (15.55)
- (15.55)
коэффициент динамичности. Он показывает во сколько раз полный максимальный прогиб больше прогиба балки от неработающего мотора.
В случае приближения частоты изменения вынуждающей силы к частоте собственных колебаний коэффициент нарастания колебаний стремится к бесконечности (если учесть силы сопротивления колебаниям, то он стремится к большой, но конечной величине). Такое явление называется резонансом. Нужно подбирать  так, чтобы не допустить резонанса в проектируемой системе.
так, чтобы не допустить резонанса в проектируемой системе.
Итак, полный прогиб во времени (15.23) будет иметь вид
 (15.56)
(15.56)
Определим максимальные напряжения при изгибе балки в точках наиболее удаленных от нейтральной оси в процессе колебаний
 (15.57)
(15.57)
где  - (15.58)
- (15.58)
максимальное напряжение от неработающего мотора,
 - изгибающий момент от единичной силы,
- изгибающий момент от единичной силы,
 (15.59)
(15.59)
По (15.45) и (15.46)
 (15.60)
(15.60)
Подставив (15.60) и (15.21) в (15.59), будем иметь
 (15.61)
(15.61)
где  - максимальное нормальное напряжение в наиболее удаленной точке сечения от амплитудного значения силы
- максимальное нормальное напряжение в наиболее удаленной точке сечения от амплитудного значения силы  , приложенной статическим образом.
, приложенной статическим образом.
Итак (15.57) примет вид
 (15.62)
(15.62)
Максимальная величина достигается в момент соблюдения (15.51)
 (15.63)
(15.63)
где  - такой же коэффициент динамичности, который учитывается для прогиба (15.55).
- такой же коэффициент динамичности, который учитывается для прогиба (15.55).
Таким образом, для того чтобы определить максимальные по величине факторы, возникающие при колебаниях, нужно статические факторы умножить на коэффициент динамичности (см. формулы (15.54) и (15.63)).
Теперь рассмотрим второй случай опирания правого конца балки – упругое опирание, балка подвешена к растянутому стержню.
При этом изменится коэффициент жесткости 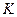 в месте прикрепления мотора. Теперь величина
в месте прикрепления мотора. Теперь величина  будет складываться из двух слагаемых: одно за счет прогиба балки на жестких опорах (как в первом случае) и перемещения балки как жесткого диска в том же сечении за счет опускания правого конца балки из-за деформации
будет складываться из двух слагаемых: одно за счет прогиба балки на жестких опорах (как в первом случае) и перемещения балки как жесткого диска в том же сечении за счет опускания правого конца балки из-за деформации  растянутого стержня (рис.15.32)
растянутого стержня (рис.15.32)
Таким образом,
 . (15.64)
. (15.64)

Рис.15.32
Введение упругой связи приводит к изменению собственной частоты системы с одной степенью свободы, изменению коэффициента нарастания колебаний  и коэффициента динамичности. При сравнении двух случаев опирания все будет зависеть от того, в каком случае ближе будут частоты
и коэффициента динамичности. При сравнении двух случаев опирания все будет зависеть от того, в каком случае ближе будут частоты  и
и  , то есть ближе резонанс. Подрессоривание в случае колебаний не обязательно улучшает напряженно-деформированное состояние балки.
, то есть ближе резонанс. Подрессоривание в случае колебаний не обязательно улучшает напряженно-деформированное состояние балки.
Дата добавления: 2015-07-12; просмотров: 80 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение напряжений при колебаниях. Резонанс | | | Пример 2. |