Собственные колебания упругих систем с конечным числом степеней свободы

В этом случае 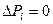, и уравнения (15.69) принимают вид

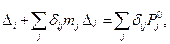(15.70)

Это система неоднородных дифференциальных уравнений второго порядка. В частном случае системы с одной степенью свободы получим:

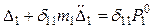(15.71)

или, так как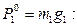

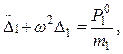(15.72)

где обозначено

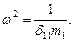(15.73)

Решение (15.72) будет:

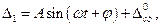(15.74)

где 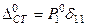- частное решение уравнения (10.8), представляющее статическое перемещение массы, 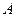- амплитуда колебания, 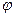- начальная фаза колебания, - круговая частота (рис. 15.37).

Время 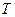одного колебательного движения точки называют периодом колебания. Величину 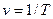, характеризующую число колебаний в единицу времени, - частотой колебаний.

Свяжем частоту колебаний 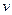с круговой частотой . Так как при изменении времени на 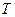система приходит, вследствие периодичности движения, в одно и то же положение, то

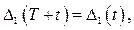
или

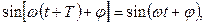
откуда имеем:

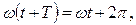
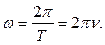(15.75)

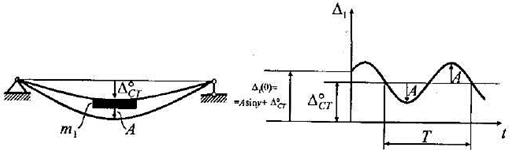
а) б)

Рис. 15.37

Максимальное перемещение

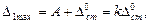(15.76)

где через

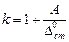(15.77)

обозначен коэффициент динамичности.

Для определения 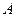необходимо задать начальные условия:

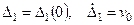при 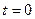. (15.78)

Тогда

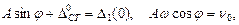
откуда

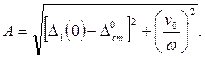(15.79)

Динамические максимальные напряжения определяются на основании закона Гука и соотношения (15.76) по формуле:

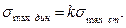(15.80)

Если число степеней свободы 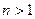, то решением (15.70) будет

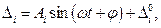(15.81)

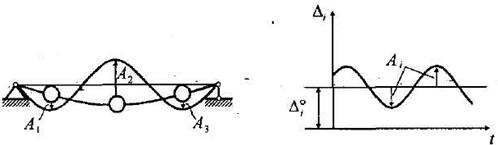
где 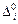- частные решения, представляющие собой статические перемещения масс 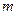, 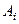- амплитуды колебании этих масс (рис. 15.38).

а) б)

Рис. 15.38

Подставляя выражения (15.81) в (15.70), найдем уравнения:

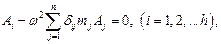(15.82)

которые служат для определения собственных частот 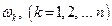колебаний упругой системы с степенями свободы.

Например, для системы с двумя степенями свободы () имеем:

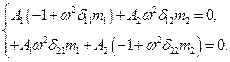(15.83)

Однородная система уравнений (15.82) имеет отличные от нуля решения только в том случае, если определитель, составленный из ее коэффициентов равен нулю:

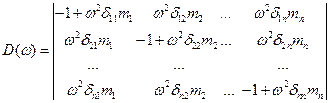(15.84)

Определитель (15.84) после раскрытия приводит к уравнению степени относительно , которое имеет корней 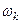. Каждый корень дает частоту собственных колебаний упругой системы, причем их можно перенумеровать так, что

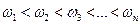(15.85)

Коэффициенты динамичности

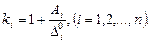(15.86)

Выше мы рассматривали собственные колебания при отсутствии сил сопротивления. При таком предположении колебания продолжаются сколь угодно долго. В действительности всегда существуют силы (сопротивления воздуха, воды и др.), направленные против движения масс и приводящие к постоянному уменьшению амплитуды 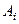собственных колебаний вплоть до остановки движения. Предположим, что силы сопротивления 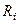пропорциональны первой степени скорости, т.е.:

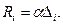
В этом случае вместо уравнений (15.70) имеем:

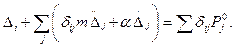(15.87)

В частном случае системы с одной степенью свободы имеем:

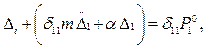(15.88)

или, в силу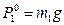

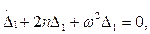(15.89)

где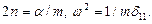

Решение уравнения можно (15.89) записать в виде:

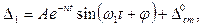(15.90)

где

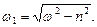(15.91)

Из (15.90) видно, что с ростом времени 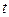амплитуда колебаний 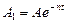уменьшается, как показано на рис. 15.39, причем частота колебаний 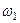мало отличается от в силу малости величины .

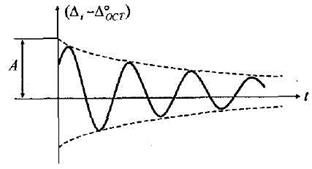
Рис. 15.39

Величина

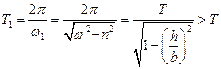(15.92)

является периодом колебаний, который больше, чем период колебаний 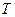в отсутствие сил сопротивления. Через период колебаний 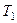отношение амплитуд будет равно:

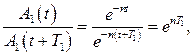(15.93)

или, логарифмируя, находим:

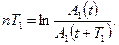(15.94)

Как видим, амплитуда убывает по закону (15.93). Величину 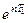называют декрементом колебаний, а величину 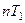- логарифмическим декрементом. Аналогичные результаты получим для упругих систем при .

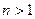Дата добавления: 2015-07-12