Вынужденные колебания упругих систем с конечным числом степеней свободы.

Возмущающие силы представим в форме:

(15.95)

где - круговая частота возмущающей силы.

В этом случае канонические уравнения движения примут вид

(15.96)

В частном случае системы с одной степенью свободы вместо (15.96) будем иметь:

(15.97)

или

(15.98)

Решением уравнения (15.98) будет:

(15.99)

где

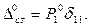(15.100)

Подставляя (15.99) в (15.98), найдем постоянную :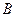

откуда

(15.101)

Если учесть трение, то собственные колебания системы, определяемые в (15.99) первым слагаемым, со временем затухнут и для установившегося режима вынужденных колебаний будем иметь:

(15.102)

Величина 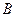представляет собой амплитуду вынужденных колебаний. Максимальное перемещение:

(15.103)

где

коэффициент динамичности. (15.104)

Максимальное динамическое напряжение

(15.105)

При имеем

Явление резкого увеличения амплитуды колебани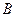й и при совпадении частот собственных колебаний и возмущающей силы носит название резонанса, а само совпадение частот:

условия резонанса. (15.106)

Возвратимся к системе с степенями свободы. Решение системы уравнений (15.96) представим в виде

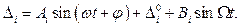(15.107)

Подставляя (15.107) в (15.96), найдем:

(15.108)

Например, для системы с двумя степенями свободы () получим:

(15.109)

Решение системы (15.108) имеет вид

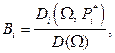(15.110)

где определяется формулой (15.84), если заменить на

При будем иметь:

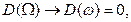(15.111)

и поэтому амплитуды вынужденных колебаний т.е. имеет место резонанс.

В технике возмущающие силы бывают известны довольно редко. Обычно известна только их частота . Поэтому задача динамического расчета упругих систем сводится к определению собственных частот свободных колебаний с целью выявления возможности резонанса.

Дата добавления: 2015-07-12