Канонические уравнения колебания упругих систем с конечным числом степеней свободы

Рассмотрим упругую систему, несущую несколько сосредоточенных масс 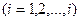. Пусть 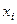- силы, приложенные к этим грузам в направлении их смещений (рис. 15.36).

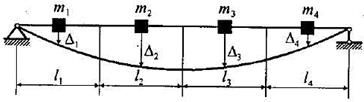
Рис. 15.36

Тогда перемещения этих грузов в направлении приложенных сил по закону Гука и принципу независимости действия сил определяются по формулам:

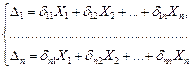(15.65)

или в сокращённой записи

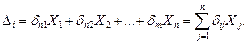(15.66)

Здесь 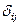- коэффициенты влияния, определяемые с помощью формулы Мора. Представим теперь, что наша система пришла в движение. Выясним природу сил 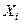в этом случае. На сосредоточенную массу может действовать внешняя сила 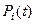, зависящая от времени и, согласно принципу Даламбера, - сила инерции 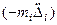. Следовательно,

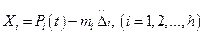(15.67)

Здесь точки над 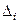означают двукратное дифференцирование по времени. В свою очередь сила может состоять из постоянной 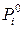(например, вес груза) и переменной 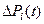частей:

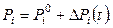(15.68)

Подставляя (15.67) в (15.66), получим форму записи уравнений движения упругих систем с конечным числом степеней свободы:

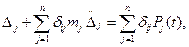(15.69)

которые называются каноническими уравнениями колебаний упругих систем. При исследовании колебаний различают собственные (свободные) и вынужденные колебания. Под собственными колебаниями системы понимают такие, которые она совершает при отсутствии внешнего силового воздействия, т.е. предоставленная самой себе. В этом случае 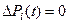, и колебания поддерживаются только упругими силами. Под вынужденными колебаниями упругой системы понимают такие, которые происходят под действием возмущающих сил .

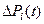Дата добавления: 2015-07-12