Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Пример 2. Определить размеры поперечного сечения консольной балки с поперечным сечением

Основные характеристики цикла и предел усталости | Основные характеристики цикла и предел усталости | Диаграмма усталостной прочности | Расчет коэффициентов запаса усталостной прочности | Влияние состояния поверхности и размеров детали на усталостную прочность | Коэффициент запаса усталостной прочности и его определение | Колебания системы с одной степенью свободы | Определение напряжений при колебаниях. Резонанс | Канонические уравнения колебания упругих систем с конечным числом степеней свободы | Собственные колебания упругих систем с конечным числом степеней свободы |


Читайте также:
  1. IV. Практические наставления. Сила и значение веры, ветхозаветные примеры веры. (10.19-13.25).
  2. V. ПРИМЕРЫ ВЫПОЛНЕНИЯ ЗАДАНИЙ
  3. А) Примеры веры древних, до потопа (11,4-7)
  4. Автономные системы примеры /экодома
  5. Аддитивное и субтрактивное смешение цветов, примеры использования.
  6. Анализ данного примера
  7. Б) Примеры веры Авраама и Сарры (11,8-19)

Определить размеры поперечного сечения консольной балки с поперечным сечением, состоящим из двух швеллеров (рис. 15.33). На балке установлен электродвигатель, имеющий несбалансированную вращающуюся массу m. Произведение радиуса дисбаланса на массу кгм. Длина балки l =1 м. Число оборотов массы n =3000 об/мин. Вес двигателя P =2000 Н. Коэффициент усиления колебаний при резонансе =32. Допускаемое напряжение материала балки 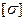= 60 МПа.

Рис. 15.33

Круговая частота возмущающей силы равна:

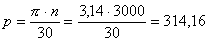1/сек.

Частота собственных колебаний для консольной балки определяется по формуле:

.

Условие прочности имеет следующий вид:

,

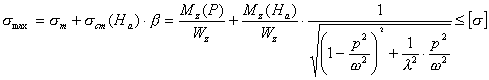Максимальные изгибающие моменты действуют в заделке и равны соответственно:

,

где амплитудное значение возмущающей (инерционной) силы равно .

Поскольку в условие прочности входят неизвестные моменты сопротивления и инерции, дальнейшие вычисления осуществляем методом последовательных приближений. Все расчеты для дорезонансной (первое приближение ) и зарезонансной (первое приближение ) областей сведены в таблицу 15.1.

Таблица 15.1.

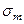№ про- филя , см4 Wz, см3 , 1/сек b , МПа , МПа , МПа , МПа
0.8 -   - 392.7 - - - - -
0.76       413.08 2.368 10.195 24.14 4.132 28.276
0.89       352.35 4.832 12.851 62.096 5.208 67.304
0.848 22a     370.26 3.554 11.639 41.368 4.717 46.085
1.2 -   - 261.8 - - -    
1.187 18a     264.6 2.43 18.692 45.454 7.576 53.030
1.427 16a       0.962 23.955 23.055 9.708 32.763
5.875 6.5 97.2   53.47 0.030 164.5 4.908 66.06 71.57
4.329     44.8 72.6 0.056 110.15 6.208 44.643 50.851

Как видно из таблицы 15.1, условию прочности отвечают для дорезонансной области швеллер номера 22а, а для зарезонансной области – швеллер номер 8. При этом вес погонного метра швеллера номера 22а в 3,2 раза больше, чем для швеллера номера 8. Кроме этого для швеллера номер 8 по сравнению с номером 22а, при примерно одинаковых максимальных напряжениях цикла, значительно меньше амплитуда напряжений цикла, что имеет существенное значение для усталостной прочности.

 

 

Дата добавления: 2015-07-12; просмотров: 68 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Пример 1.| Степень свободы колеблющейся системы
mybiblioteka.su - 2015-2024 год. (0.007 сек.)