Диаграмма усталостной прочности

Положим, имеется машина, на которой можно производить усталостные испытания в условиях любого несимметричного цикла. Задавая постоянное значение 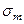, находим путем последовательных испытаний образцов такое наибольшее значение амплитуды 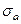, при котором материал способен еще выдержать неограниченное число циклов. Если для взятого материала такого предельного напряжения не существует, величина 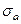определяется по условному базовому числу N.

В результате проведенной серии испытаний устанавливается предельное значение 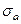, соответствующее некоторому напряжению 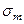. Полученный результат может быть графически изображен точкой в системе координат 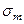, 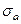(рис.15.10). Сумма координат этой точки дает предельное максимальное напряжение цикла, т. е. предел усталости 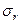, где:

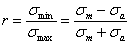
Продолжая такие испытания и дальше, получаем множество точек, через которые проводится предельная кривая, характеризующая прочностные свойства материала в условиях несимметричных циклов. Эта кривая носит название диаграммы усталостной прочности (рис.15.11).

Точки А и С диаграммы соответствуют пределам прочности при простом растяжении и сжатии. Точка В отражает результаты испытания в условиях симметричного цикла.

Полученная диаграмма дает возможность судить о прочности конструкции, работающей при циклически изменяющихся напряжениях.

Положим, для некоторой детали цикл характеризуется значениями напряжени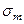й и 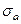. Эти величины могут рассматриваться как координаты рабочей точки в плоскости 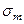, 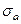. Если рабочая точка располагается ниже предельной кривой, рассматриваемая деталь может в условиях циклически изменяющихся напряжений работать неограниченно долго. Если рабочая точка оказывается выше предельной кривой, деталь разрушится после некоторого числа циклов.

Так как построение диаграммы усталостной прочности связано с весьма трудоемкими испытаниями, предпочитают обычно полученную кривую АВС заменять двумя прямыми АВ и ВС, как это отмечено пунктиром на рис.15.11. Рабочая область при этом несколько сокращается, что дает погрешность в запас прочности.

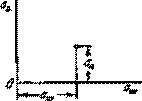
Рис.15.10. Реализация предельного напряжения.

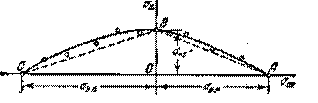
Рис.15.11. Диаграмма усталостной прочности.

Одновременно отсекается сомнительная зона разброса экспериментальных точек.

Для построения упрощенной диаграммы достаточно располагать пределом усталости при симметричном цикле 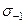, и иметь значения пределов прочност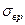и и .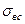

Рабочая точка в плоскости 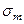, 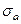не может занимать произвольное положение. Она должна находиться в области осуществимых циклов, которая определяется следующими очевидными условиям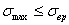и:

и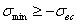

Так как:

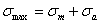, а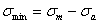

то область осуществимых циклов имеет верхнюю границу в виде двух прямых:

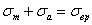и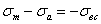

Эти прямые вместе образуют треугольник АСD (рис.15.12), который и представляет собой область осуществимых циклов.

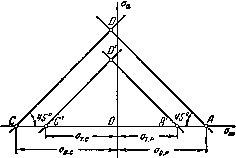
Рис.15.12. Область осуществимых циклов

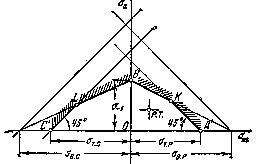
Рис.15.13. Область допустимых циклов с ограничениями на пластические деформации.

Для пластичных материалов таким же способом может быть отмечена область упругих деформаций. Граница этой области очерчивается сверху прямым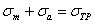и:

и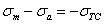

В результате получаем треугольник 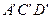(рис.15.12).

Если рабочая точка оказывается в пределах этого треугольника» пластические деформации в детали не возникают. Рабочая точка, находящаяся за пределами треугольника 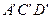, но остающаяся внутри треугольника АСD, свидетельствует о том, что в детали возникают пластические деформации. Если, наконец, рабочая точка оказывается за пределами треугольника АСD, при первом же цикле происходит разрушение детали.

При расчетах конструкций, предназначенных на длительные сроки службы, напряжения цикла ограничиваются как по условиям усталостной прочности, так и по условиям недопущения пластических деформаций. Поэтому, объединяя диаграммы, показанные на рис.15.11 и 15.12, получаем рабочую область в виде многоугольника А'КВLС' (рис.15.13). Рабочая точка (р.т.) исследуемого цикла для рассчитываемой детали должна находиться в пределах указанного многоугольника.

Теперь возникает вопрос, как определить координаты рабочей точки и как определить коэффициент запаса детали в условиях циклического нагружения. Оба эти вопроса содержат в своем решении ряд специфических особенностей, к рассмотрению которых сейчас и перейдем.

Дата добавления: 2015-07-12