Колебания системы с одной степенью свободы

Упругими колебаниями называют движения упругих тел, представляющие собой периодические отклонения их относительно положения равновесия.

При исследовании колебаний упругих систем различают собственные (свободные) и вынужденные колебания. Под собствен­ными колебаниями понимается движение системы при отсутствии внешних воздействий. Если колебание системы сопровождается действием внешних сил, то движение называется вынужденным.

В динамических расчетах важным понятием является число степеней свободы системы – наименьшее количество независимых геометрических параметров, определяющих положение всех масс системы в произвольный момент времени. Системами с одной степенью свободы будут такие, у которых для полной фиксации их геометрического состояния в любой момент времени достаточно знать один параметр, например, положение определенной точки. Таковы, например, растянутая или сжатая незначительного веса пружина с грузом на конце, совершающая продольные колебания; небольшого (сравнительно с грузом Q) собственного веса балка, изображенная на рис.15.24, колеблющаяся в направлении, перпендикулярном к ее оси, и т. п.

Рис.15.24

Простейшим видом колебаний являются гармонические колебания, которые описываются тригонометрическими функциями синуса или косинуса, например,

(15.4)

где А ₀ – амплитуда, т.е. максимальное значение обобщенной координаты x при колебаниях системы (рис. 15.25); – круговая частота свободных колебаний; – фаза колебаний; 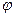– начальная фаза колебаний, т.е. фаза в момент времени t = 0.

Промежуток времени за который совершается полный цикл ко­лебаний, носит название периода собственных или вынужденных колебаний, смотря по тому, о каких колебаниях идет речь. Период колебаний обозначается через Т. Величина обратная Т, называется частотой колебаний:

,

и представляет собой число колебаний в течение одной секунды. В технике в большинстве случаев используется понятие круговой частоты , представляющей собой число колебаний за 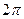секунд.

Период колебаний и круговая частота свободных колебаний связаны зависимостью

(15.5)

Круговая частота связана с сосредоточенной массой m и жесткостью с системы зависимостью

(15.6)

Жесткость системы – это сила, которая вызывает перемещение, равное единице. Часто масса колеблющейся системы считается постоянной, а упругая система линейной, для которой сила упругости Р = mg (g – ускорение свободного падения) пропорциональна соответствующему перемещению , т. е.

(15.7)

Учитывая приведенные выше соотношения, можно записать формулы для круговой частоты и периода свободных колебаний, каждая из которых в том или ином случае может оказаться удобной при решении практических задач:

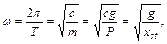(15.8)

(15.9)

Возможны системы с несколькими упругими связями, каждая из которых имеет свою жесткость. На рис. 15.26, а показана схема механической системы с так называемым параллельным соединением упругих связей с жесткостями и , а на рис. 15.26, б – с последовательным соединением упругих связей. Суммарные жесткости показанных систем рассчитываются по-разному.

При параллельном соединении упругих связей жесткость системы рассчитывается по формуле

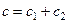, (15.10)

а при последовательном соединении

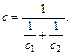(15.11)

В предыдущих формулах под массой m понимается масса груза, совершающего колебания, без учета собственной массы системы. В остальных задачах принято, что масса m состоит из массы груза, совершающего колебания, и приведенной к точке распределенной собственной массы системы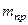

, (15.12)

где , – истинная собственная масса системы; – коэффициент привидения. Принимаем подобно коэффициенту приведения при ударной нагрузке – при продольных колебаниях систем, типа показанной на рис. 15.27, а; 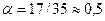– для изгибных колебаний шарнирно опертой балки на двух опорах (рис. 15.27, б); 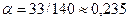– для изгибных колебаний консоли (рис. 15.27, в).

Дата добавления: 2015-07-12