Приближенные методы определения низших частот собственных колебаний упругих систем

В большем числе случаев собственная распределенная масса 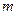упругих систем оказывается соизмеримой с присоединенными сосредоточенными массами. Поэтому сведение систем с бесконечным числом степеней свободы к системам с малым конечным числом степеней свободы оказывается не всегда приемлемым. В этих условиях предпочтительнее являются приближенные методы. Рассмотрим один из них – энергетический метод Релея.

Пусть имеется некоторая колебательная упругая система (рис.15.40, а) несущая собственный вес и несколько сосредоточенных масс . Наиболее опасной является первая форма колебаний, когда все массы колеблются в одной фазе (изогнутая ось 1 на рис. 15.40, б). В этом случае перемещения и напряжения в системе - наибольшие (мы отвлекаемся здесь от вопроса усталости материала, для которого существенными могут оказаться колебания с высокой собственной частотой).

Рассмотрим первую форму колебаний упругой системы. Если рассматривать колебания относительно статического положения равновесия системы, то закон движения любой точки упругой системы можно записать в виде

(15.112)

а) б)

Рис. 15.40

Перемещение массы 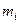будет:

(15.113)

На основании закона сохранения энергии для любых двух положений системы имеем:

(15.114)

где 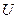- потенциальная энергия упругой системы,

(15.115)

кинетическая энергия системы.

Рассмотрим в качестве первого положения такое, при котором все массы проходят статическое положение равновесия. В этом положении и потенциальная энергия 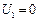. Скорость

(15.116)

достигает максимального значения

(15.117)

Поэтому максимального значения достигает кинетическая энергия системы:

(15.118)

В качестве второго положения рассмотрим момент наибольшего отклонения системы от статического положения равновесия, когда кинетическая энергия , а потенциальная достигает своего максимального значения , равенство (15.114) можно теперь написать на основании вышеприведенных рассуждений в виде :

откуда получаем формулу Релея:

(15.119)

Для вычисления необходимо знать форму деформированного состояния упругой системы. Если задать ее приближенно, то этим самым мы как бы накладываем на систему дополнительные связи, т.е. делаем ее более жесткой. Вычисленная при этом частота со будет несколько завышенной по сравнению с точным значением. Если форму деформированного состояния угадать точно, то формула Релея даст точное значение низшей частоты колебаний упругой системы.

В случае изгиба балки для вычисления и имеем формулу:

(15.120)

В случае растяжения – сжатия стержня:

(15.121)

так как

(15.122)

Для случая кручения:

(15.123)

так как

(15.124)

Дата добавления: 2015-07-12