Читайте также:
|
Рассмотрим упругую систему, например балку с распределенной массой (рис. 15.41, а). Поставим следующую задачу. Какую массу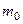 
нужно приложить в некоторой точке 
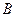такой же, но невесомой балки (рис. 15.41, б), чтобы низшие частоты колебаний исходной и упрощенной систем были одинаковы. Точку 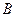назовем точкой приведения массы системы, а массу 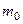- приведенной массой.
а) б)
Рис. 15.41
Если 
- коэффициент жесткости системы, то ее потенциальная энергия:
(15.125)
Подставляя (15.125) в формулу Релея (15.119), получим:
(15.126)
С другой стороны, для системы с одной степенью свободы имеем
(15.127)
Сравнивая (15.126) и (15.127), получим:
(15.128)
Дата добавления: 2015-07-12; просмотров: 90 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Приближенные методы определения низших частот собственных колебаний упругих систем | | | Устойчивость вращающихся валов |