Читайте также:
|
Рассмотрим поперечные колебания балки постоянного сечения с площадью F (рис. 15.50).
Рис. 15.50
Участок балки длиной 
имеет массу 
где 
- плотность материала. Воспользуемся дифференциальным уравнением изогнутой оси балки четвертого порядка статической задачи: 
(15.171)
При рассмотрении динамической задачи мы должны считать, что прогиб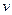 
является функцией двух переменных 
и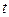 
. Нагрузка 
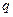также должна зависеть от координаты и времени 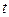. Учитывая только инерционную силу 
и используя принцип Даламбера, вместо (15.171) получаем дифференциальное уравнение поперечных колебаний балки:
(15.172)
Как и в случае продольных колебаний, решение задачи ищем в виде:
(15.173)
Можно считать 
Тогда после подстановки (15.173) в (15.172), получим уравнение
(15.174)
где
(15.175)
Решение уравнения (15.174) имеет вид
(15.176)
Постоянные А, В, С, D находим из граничных условий на опорах:
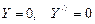при 
,
при 
. (15.177)
Из первых двух условий имеем 
. Из двух других находим:
(15.178)
Приравнивая нулю определитель системы уравнений (15.178), получим:
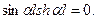(15.179)
Так как 
только при 
, то остаётся принять:
или, согласно (15.175),
(15.180)
Из (15.178) при 
и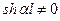 
следует 
. Таким образом, при изгибных колебаниях балки образуется бесконечное число частот собственных колебаний, пропорциональных 
, где 
– число полуволн изогнутой оси балки. Прогибы балки:
(15.181)
При колебаниях в основном тоне балка изгибается по одной полуволне (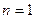
). При 
имеем две полуволны, при 
– три (рис. 15.50).
Колебания балки в основном тоне (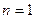) можно использовать для определения динамического модуля упругости материала, из которого изготовлена балка. Из (15.180) получаем:
(15.182)
где 
- частота колебаний.
Дата добавления: 2015-07-12; просмотров: 319 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Продольные колебания стержня | | | Расчет на прочность при нерегулярной переменной нагруженности |