Удар по конструкции вертикально движущимся телом

Для наглядности рассмотрим не произвольную упругую систему, а тяжелую балку (рис. 15.44, а), на которую с высоты 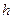падает груз массой 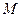. Выберем у балки точку 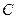, в которой происходит удар, за точку приведения массы и заменим балку с распределенной массой 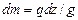( 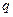- вес единицы длины балки, 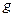- ускорение свободного падения) балкой с одной приведенной массой 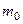(рис.15.44, б), т.е. заменим упругую систему с бесконечным числом степеней свободы на систему с одной степенью свободы. Обозначим через:

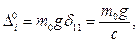(15.132)

статический прогиб балки, соответствующий точке 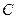в системе с приведённой массой, 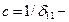жёсткость балки.

Пусть - скорость падающего тела в момент удара, а 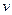- скорость приведённой массы и «прилипшего» к нему падающего тела сразу после удара. Если груз падает с высоты 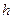, то 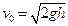. Из условия сохранения количества движения системы имеем:

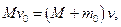
откуда

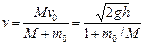(15.133)

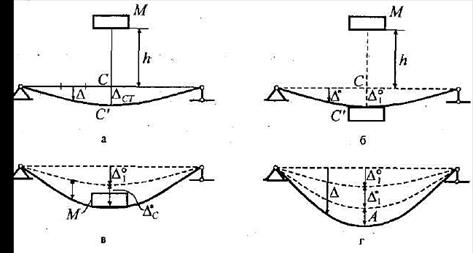
Рис. 15.44

Скорость 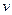будет, с другой стороны, начальной скоростью объединенной массы 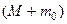в ее колебательном движении после удара (2-й этап).

Пусть 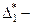статический прогиб балки в точке 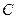от веса падающего груза 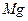, т.е.

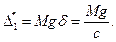(15.134)

Тогда полный статический прогиб:

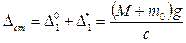(15.135)

После удара начнётся колебательное движение упругой системы. По закону сохранения энергии сумма кинетической и потенциальной энергии системы при максимальном отклонении от статического положения равновесия перейдёт в потенциальную энергию деформации упругой системы:

,

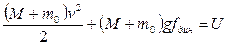где 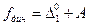динамическое перемещение после удара,

,

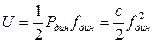т.к. 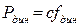по закону Гука; – жёсткость упругой системы.

В результате получаем уравнение:

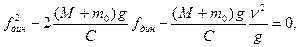
или, с учётом (15.133) – (15.135):

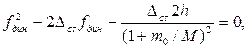
Решая полученное квадратное уравнение, находим:

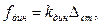
где

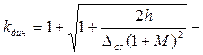(15.136)

динамический коэффициент.

В частности при внезапном ударе () имеем .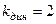

Можно иначе определить динамический коэффициент. Дифференциальное уравнение свободных колебаний системы после удара будет:

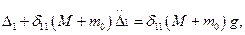
или

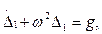(15.137)

где

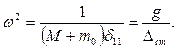(15.138)

Решением уравнения (15.137) будет:

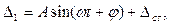(15.139)

где

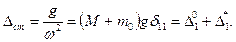
Закон движения (15.139) представлен на рис. 15.45.

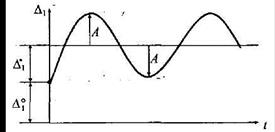
Рис. 15.45

Начальные условия колебательного движения системы после удара

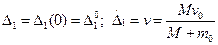при 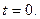(15.140)

Удовлетворяя решение (15.140) этим условиям, найдем:

или

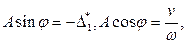
откуда находим:

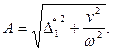(15.141)

Найдем теперь максимальное отклонение системы от исходного состояния в ее колебательном движении:

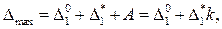(15.142)

Соотношение (15.142) можно записать

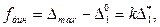(15.143)

где

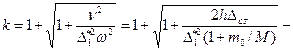(15.144)

коэффициент динамичности. Он показывает во сколько раз прогиб от удара больше прогиба при статическом приложении того же груза.

Если 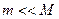, то ,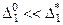

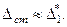
В этом случае динамический коэффициент (105.144) принимает вид:

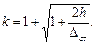(15.145)

Выражение (15.144) совпадает с (15.136) при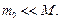

По закону Гука

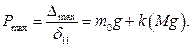
Следовательно, максимальное напряжение

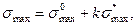(15.146)

где 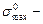напряжение в балке до удара груза 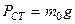, 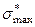- статическое напряжение от груза 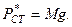При 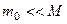имеем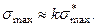

Дата добавления: 2015-07-12