
|
Читайте также: |
& Литература: [1], [3], [8], [7].
Теория возмущения – метод приближенного решения задач квантовой механики, аналогичный тому, который в классической физике используется при расчетах движения космических тел.
Теория возмущения в квантовой механике применяется в тех случаях, когда гамильтониан может быть представлен в виде:  =
=  0 +
0 +  , где слагаемое
, где слагаемое  0 описывает наиболее существенные взаимодействия, а оператор возмущения
0 описывает наиболее существенные взаимодействия, а оператор возмущения  – менее существенное. Например, взаимодействие электрона с ядром атома водорода более существенно по сравнению с его взаимодействием с полями, в которых реально находится атом. Теория дает верный результат, если менее существенное взаимодействие (возмущение) достаточно мало. Она же устанавливает и количественный критерий малости возмущения.
– менее существенное. Например, взаимодействие электрона с ядром атома водорода более существенно по сравнению с его взаимодействием с полями, в которых реально находится атом. Теория дает верный результат, если менее существенное взаимодействие (возмущение) достаточно мало. Она же устанавливает и количественный критерий малости возмущения.
Стационарная теория возмущения предполагает, что оператор  точно так же, как и
точно так же, как и  0, не зависит от времени, и поэтому ищется решение стационарного уравнения Шредингера:
0, не зависит от времени, и поэтому ищется решение стационарного уравнения Шредингера:
 |Y> = |Y> E. (26.1)
|Y> = |Y> E. (26.1)
Сначала задача решается в нулевом приближении, то есть полагается  = 0, и находятся собственные значения En(0), а также собственные векторы |n> оператора
= 0, и находятся собственные значения En(0), а также собственные векторы |n> оператора  0:
0:  0 |n> = |n> En(0). (26.2)
0 |n> = |n> En(0). (26.2)
Квантовое число n может принимать значения n = 1, 2, …. Соотношение (26.2) предполагает, что вырождение отсутствует. В этом случае искомые величины E и |Y> можно представить в виде степенных рядов по параметру l, определяющему малость возмущения ( = l
= l 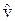 ):
):
E = En(0) + l E(1) + l2 E(2) + …, (26.3)
|Y> = |n> + |Y(1)> l + |Y(2)> l2 + …. (26.4)
Подставляя эти ряды, а также (26.2) в (26.1) и сравнивая коэффициенты при одинаковых степенях l, можно найти поправки к энергии и к амплитудам состояния, обусловленные возмущением. В частности, поправка к энергии в первом приближении оказывается равной:
DE(1) = l E(1) = <n|  |n> =
|n> = 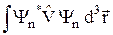 , (26.5)
, (26.5)
где Yn( ) – волновая функция состояния |n>.
) – волновая функция состояния |n>.
Поправка к энергии во втором приближении –
DE(2) = l2 E(2) = 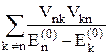 ,
,
где Vnk = <n|  |k> =
|k> = 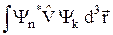 . Квантовое число k = 1, 2, ….
. Квантовое число k = 1, 2, ….
Критерий применимости теории получается из требования, чтобы выполнялось неравенство |DE(2)| << |DE(1)|, последнее будет обеспечено, если
|DE(1)| << |En(0) – Ek(0)|. (26.6)
Это означает, что поправка к энергии, даваемая теорией, должна быть много меньше разности уровней невозмущенной ( = 0) системы.
= 0) системы.
При наличии вырождения одному собственному значению E(0) оператора  0 соответствует g (кратность вырождения) собственных векторов |s>, где s = 1, 2, …, g:
0 соответствует g (кратность вырождения) собственных векторов |s>, где s = 1, 2, …, g:  0 |s> = |s> E(0). (26.7)
0 |s> = |s> E(0). (26.7)
В этом случае нельзя использовать степенной ряд (26.4), поскольку его нулевой член не определен. Приближение основывается на ином подходе. Искомый вектор |Y> разлагают по всем собственным векторам |k> оператора  0, но ограничиваются только теми членами разложения, которые соответствуют рассматриваемому уровню E(0):
0, но ограничиваются только теми членами разложения, которые соответствуют рассматриваемому уровню E(0):
|Y> = 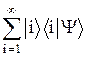 »
» 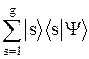 = |Y0>. (26.8)
= |Y0>. (26.8)
Смысл такого приближения помогает уяснить простая аналогия. Геометрический вектор, образующий малый угол с координатной плоскостью x0y, можно приближенно заменить его составляющей, лежащей в этой плоскости. Иными словами, можно пренебречь одним из членов разложения по трехмерному базису.
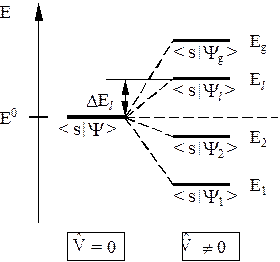 Рис. 26.1
Рис. 26.1
|
Уравнению (26.7) удовлетворяют не только векторы |s>, но и их произвольная суперпозиция, в том числе и |Y0>:
 0 |Y0> = |Y0> E0. (26.9)
0 |Y0> = |Y0> E0. (26.9)
Подставляя в (26.1) |Y> = |Y0>, E = E0 + DE, а также (26.9), получим:
 |Y0> = |Y0> DE. (26.10)
|Y0> = |Y0> DE. (26.10)
Это уравнение определяет те коэффициенты <s|Y> разложения |Y0>, которые делают (26.8) приближенным решением исходного уравнения (26.1). Подставив (26.8) в (26.10) и умножив на вектор |k>, где k = 1, 2, …, g, получим после преобразований:
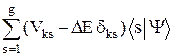 = 0. (26.11)
= 0. (26.11)
Здесь Vks = <k|  |s>. (26.12)
|s>. (26.12)
Выражение (26.11) представляет собой однородную систему линейных алгебраических уравнений относительно неизвестных <s|Y>. Такая система, как известно из алгебры, имеет отличные от нуля решения лишь при условии: Det (Vks – DE dks) = 0. (26.13)
Полученное, так называемое, секулярное уравнение имеет g корней DE l, где l = 1, 2, …, g. Таким образом, рассматриваемый g-кратно вырожденный уровень при учете возмущения расщепляется на g, вообще говоря, различных подуровней, что иллюстрирует рисунок 26.1.
Для каждого из найденных подуровней получается своя система уравнений (26.11), из которой найдется своя совокупность коэффициентов <s|Y l >0, определяющая соответствующее состояние |Y l 0>. Так что вырождение снимается: различным подуровням соответствуют различные состояния.
Критерий применимости теории возмущения при наличии вырождения аналогичен критерию (26.6): поправки к энергии DE l должны быть по модулю много меньше разности энергий рассматриваемого уровня и соседних.
Теория стационарных возмущений позволяет, в частности, объяснить нормальный и аномальный эффекты Зеемана, расщепление спектральных линий при помещении атома в постоянное электрическое поле (эффект Штарка). Применяется она и при описании свойств многоэлектронных атомов и молекул.
? Контрольные вопросы
1. В чем заключается и для чего применяется теория возмущения?
2. Какие задачи решаются стационарной теорией возмущения?
3. Как находятся поправки к энергии в теории возмущения при отсутствии вырождения?
4. Как учитывается малость возмущения при наличии вырождения?
5. Расскажите о расщеплении энергетического уровня и о снятии вырождения.
25.4. Каков критерий применимости теории стационарных возмущений?
|
25.1. Найдите поправки к энергии и к амплитуде состояния в первом приближении теории возмущения при отсутствии вырождения.
25.2. Получите формулу для поправки к энергии во втором приближении теории возмущения при отсутствии вырождения.
25.3. Найдите энергетические уровни атома водорода в первом возбужденном состоянии, помещенного в однородное постоянное электрическое поле напряженностью x. Воспользуйьесь тем свойством функций Y2 l m, что если l ¢ ¹ l и m¢ = m, то ò Y2 l m* r cos(q) Y2 l ¢m¢ d3  = –3 r0, а в остальных случаях такой интеграл равен нулю.
= –3 r0, а в остальных случаях такой интеграл равен нулю.
25.4. Вычислите расщепление энергетических уровней атома в магнитном поле, энергия взаимодействия которого с магнитным моментом меньше энергии спин-орбитального взаимодействия.
25.5. Вычислите расщепление энергетических уровней атома в магнитном поле, энергия взаимодействия которого с магнитным моментом больше энергии спин-орбитального взаимодействия.
25.6. Некоторая спектральная линия возникает в результате перехода 2p3/2 ® 2s1/2. На сколько составляющих расщепляется эта линия в слабом магнитном поле? Возможны лишь такие переходы, при которых
Dj = ±1, 0 и Dm = ±1, 0.
Дата добавления: 2015-07-11; просмотров: 299 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Энергетический спектр и пространственная структура атома водорода. Влияние спина электрона на энергетический спектр | | | Теория нестационарных возмущений |