Теория нестационарных возмущений

& Литература: [1], [8], [7].

В теории нестационарных возмущений рассматривается система, гамильтониан которой содержит оператор возмущения (t), зависящий от времени: = ₀ + (t). (27.1)

Приходится решать не стационарное, а полное уравнение Шредингера:

Y = i ħ 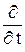Y. (27.2)

Гамильтониану нулевого приближения ₀ соответствуют стационарные состояния, волновые функции Y_n которых удовлетворяют уравнениям:

₀Y_n = i ħ 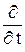Y_n. (27.3)

Стационарные состояния Y_n образуют полный базис, по которому можно разложить искомую волновую функцию:

Y = 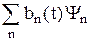. (27.4)

Задача сводится к нахождению коэффициентов разложения b_n(t).

Подставляя (27.1), (27.3) и (27.4) в (27.2), получим:

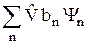= i ħ 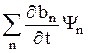. (27.5)

Умножим это равенство на Y_k^* и проинтегрируем по всему пространству. Учтем, что 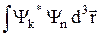= d_kn, и обозначим 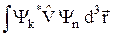= V_kn. Тогда получим: 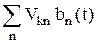= i ħ 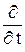b_k(t). (27.6)

Пусть в начальный момент система находилась в i-ом стационарном состоянии. Тогда Y(0) = 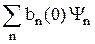= Y_i Þ b _n (0) = d _{n i}. (27.7)

В произвольный момент времени t

b_n(t) = b_n(0) + b_n⁽¹⁾(t) + b_n⁽²⁾(t) +…» d _{n i} + b_n⁽¹⁾(t). (27.8)

Приближение (27.8), конечно, предполагает, что |b_n⁽²⁾(t)| << |b_n⁽¹⁾(t)| << 1. Это выполняется при достаточно малом возмущении.

Подставляя приближение (27.8) в (27.6) и пренебрегая |b_n⁽¹⁾| по сравнению с 1, получим: b_k⁽¹⁾(t) = – 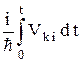. (27.9)

Квадрат модуля найденного коэффициента определяет вероятность w_ki того, что к моменту времени t система из исходного i-го состояния перейдет в k-е: w_ki(t) = |b_k(t)|² = |b_k⁽¹⁾(t)|², k ¹ i. Обычно вычисляют вероятность W_ki перехода из i-го состояния в k-е в среднем за единицу времени:

W_ki = .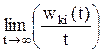

Для возмущения, описываемого гармонической функцией,

= ₀() exp (i w t), (27.10)

получается выражение:

W_ki = 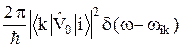, (27.11)

где w_ik = (E_i – E_k) / ħ. (27.12)

В формулу (27.11) входит d-функция. Это означает, что переходы носят резонансный характер: они происходят только при совпадении частоты возмущения w с величиной w_ik (27.12). Учет конечности ширины k-го уровня несколько сглаживает остроту резонанса: переход можно считать возможным, если (w – w_ik) ħ не превышает половину ширины уровня G. На рисунке 27.1 сплошной линии со стрелкой показан возможный переход ((w – w_ik) ħ < G/2), а пунктирной – не возможный. Вероятность перехода на уровень конечной ширины оказывается равной

W_ki = 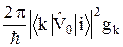, (27.13)

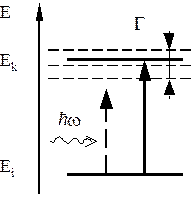Рис. 27.1

где g_k – кратность вырождения этого уровня.

Теория нестационарных возмущений описывает, в частности, переходы, происходящие в атомах под действием световых волн. В этом случае оператор возмущения имеет вид:

= =

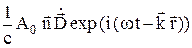= = ₀ exp (i w t), (27.14)

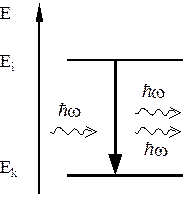Рис. 27.2

где A₀ 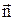– амплитуда векторного потенциала электромагнитного поля, w – частота, а 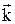– волновой вектор световой волны, 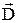= – e – дипольный момент атома. Если l = 2 p / k >> r, то оператор ₀ в (27.14) можно положить равным ₀» 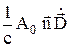. (27.15)

Это выражение лежит в основе, так называемого, дипольного приближения.

Формула (27.13) для возмущения (27.14) в дипольном приближении (14.15) принимает вид:

W_ki = 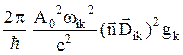, (27.16)

где 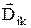= = 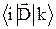– – 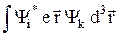(27.17)

матричные элементы дипольного момента атома. Эта формула описывает переход атома из i-го состояния в k-е под действием электромагнитной волны, частота которой отличается от w_ik (27.12) не более, чем на половину ширины уровня, деленной на ħ.

Если переход происходит в состояние с большим значением энергии (E_k > E_i), то при этом поглощается фотон с энергией ħ w_ik – имеет место резонансное поглощение (рис. 27.1). Переход на более низкий уровень сопровождается излучением такого же фотона, который вызывает этот процесс – происходит индуцированное излучение (рис. 27.2). Число фотонов в процессе индуцированного излучения увеличивается, причем все они оказываются тождественными. Последнее обстоятельство обуславливает высокую пространственную и временную когерентность лазерного излучения.

При A₀ = 0 формула (27.16) дает W_ki = 0. Казалось бы, это противоречит факту спонтанных переходов. Однако согласно квантовой электродинамике в основном состоянии электромагнитного поля (при отсутствии излучения) происходят нулевые колебания вакуума, подобные нулевым колебаниям гармонического осциллятора, вследствие чего A₀ ¹ 0. Поэтому формула (27.16) позволяет вычислить и вероятность спонтанных переходов, если взять из квантовой электродинамики величину A₀, характеризующую нулевые колебания вакуума.

На основе формулы (27.16) можно вычислить и вероятности переходов, соответствующих равновесному излучению, содержащему волны всех возможных направлений распространения и ориентаций плоскости поляризации. Так получаются коэффициенты Эйнштейна для спонтанных A_ki и индуцированных B_ki переходов:

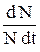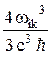
A_ki = – = 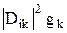, (27.18)

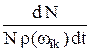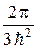
B_ki = – = 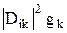. (27.19)

Здесь – dN / N – доля атомов, совершающих за время dt переходы из i-го состояния в k-е, соответственно, спонтанно или под действием равновесного излучения спектральной плотностью r(w_ik). Формулы (27.18) и (27.19), естественно, согласуются с формулой Планка для равновесного излучения.

Из (27.18) следует, что интенсивность спонтанного излучения I ~
ћ ω A_ki ~│D_ik│².Так что проблема нахождения интенсивности спектральных линий сводится к вычислению матричных элементов дипольных моментов, то есть интегралов (27.17). Центральная симметрия атома приводит к тому, что далеко не все такие интегралы отличны от нуля. Не нулевыми оказываются интегралы, соответствующие переходам, для которых

D l = l _k – l _i = ±1; (27.20)

Dj = j_k – j_i = 0, ±1; (27.21)

Dm = m_k – m_i = 0, ±1; (27.22)

DS = S_k – S_i = 0; Dσ = σ_k – σ_i = 0. (27.23)

Соотношения (27.20) – (27.23) называют правилами отбора. Переходы, для которых эти соотношения не выполняются, являются запрещенными, их вероятность равна нулю, если принять дипольное приближение. Если же не ограничиваться этим приближением, то вероятность запрещенного перехода оказывается отличной от нуля, она много меньше вероятности разрешенных переходов. Состояния, переходы с которых в дипольном приближении запрещены, называют метастабильными. Они характеризуются сравнительно большими временами жизни. Благодаря наличию метастабильных состояний удается осуществить инверсию населенности энергетических уровней, необходимую для работы лазеров.

? Контрольные вопросы

1. Приведите пример задачи, при решении нужно применить теорию нестационарных возмущений. Что в этой задаче выражает оператор возмущения?

2. Расскажите о том, как в теории нестационарных возмущений решается уравнение Шредингера.

3. Как находится вероятность перехода из одного состояния в другое под действием заданного нестационарного возмущения?

4. Расскажите о резонансном характере переходов под действием нестационарного возмущения.

5. В чем суть дипольного приближения в теории излучения атомов?

6. Расскажите об индуцированных переходах и о соответствующем коэффициенте Эйнштейна.

7. Расскажите о спонтанных переходах и о нахождении для них коэффициента Эйнштейна.

8. Расскажите о правилах отбора для излучающих атомов. Из каких соображений они получаются?

9. Расскажите о метастабильных состояниях.

F

Задания

25.7. Получите выражение (27.5).

25.8. Выведите уравнение (27.6).

25.9. Получите формулу (27.9).

25.10. Зная коэффициент Эйнштейна для спонтанного перехода A, найдите зависимость от времени интенсивности излучения возбужденного газа. Предложите способ экспериментального определения коэффициента A.

Дата добавления: 2015-07-11