Метод слоистой выборки (МСВ).

Методы прямой статистической имитации получили в научной литературе название методов Монте-Карло (ММК). При оценках надежности ошибка метода определяется выражением

Так, при R_s = 0,891 и N = 100, e= 0,03116.

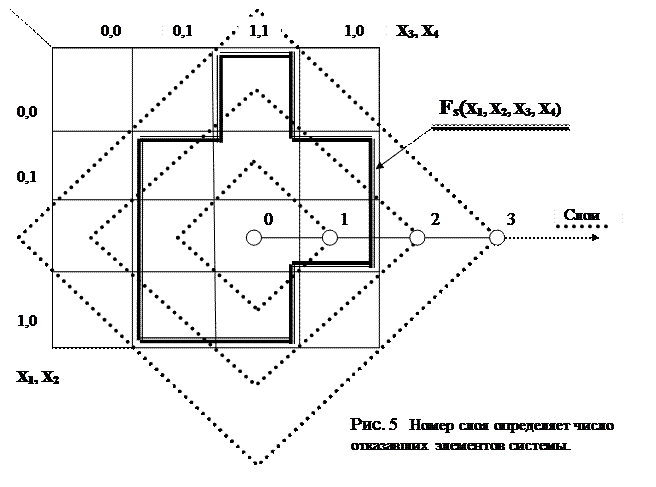
Для снижения дисперсии результатов имитационного эксперимента используют аналитико-статистические методы расчета R_s. Одним из таких методов является МСВ, иногда его называют методом «пропорциональной» выборки. Идея метода заключается в том, что все пространство состояний системы разбивается на слои (рис. 5) так, чтобы в слое дисперсия вероятностных мер была малой.

	1,1

В каждом слое проводятся статистические испытания, причем число испытаний N_i в i-м слое пропорционально вкладу данного слоя в общую вероятностную меру R_s. В расчетах надежности индекс слоя определяется числом отказавших элементов в системе. Так, если СЭЭС состоит из m элементов, то основная аналитическая формула принимает вид:

(12)

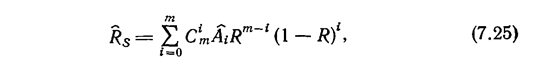
где А - живучесть, определяется статистически как вероятность отказа системы при отказе ровно i ее элементов, тогда дисперсия R_s определится из выражения

(13)

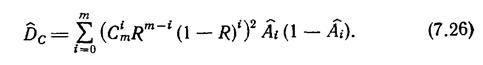
Пусть ФАЛ системы F = X₁(X₂ v Х₃). Вероятность безотказной работы

всех элементов одинакова R=0,9, тогда точное аналитическое выражение дает

Rs=(2-R)R²=0,891.

При использовании МСВ прежде всего проводят статистическую оценку условных вероятностей A_i. Непосредственно из ФАЛ видно, что A₀=1; A₁ = 2/3; А₂ = 0. Что позволяет определить точное значение дисперсии

D = (C¹₃ * 0,9(1 - 0,9))² * 2/3 (1 - 2/3);

D= 0,013122;

Видно, что по сравнению с МНК стандартную ошибку удалось понизить почти в 3 раза. Однако, при практическом использовании МСВ априори неизвестны A_i; и неизбежны бесполезные статистические испытания, например, во втором слое, в котором нет работоспособных состояний.

Дата добавления: 2015-10-16