Генераторы псевдослучайных чисел с равномерным распределением.

Источниками псевдослучайных чисел в ЭВМ являются специальные алгоритмы. Как правило, любой закон распределения случайных чисел, воспроизводимый за счет имитации, строится на основе генераторов, дающих равномерное распределение в диапазоне 0.. 1.

Равномерное распределение характеризуется плотностью

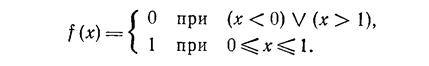
Рассмотрим алгоритм генерации псевдослучайных чисел, основанный на сложении двух случайных чисел по модулю 4, после сложения остается остаток от деления суммы на 4, который и принимают за новое случайное число. Последующая нормировка (деление на 4) приводит к появлению чисел, изменяющихся в диапазоне 0..1.

Программа 1/34. Генерация псевдослучайного числа с равномерным распределением в диапазоне (0..1).

	ИП1	ИП2	П1	+	П3		-	Fx>0		П3
	ПИ3	П2		¸	С/П	БП

Инструкция: p=Р1; 0,5421019 =Р2; В/О; С/П; РХ = RAV. Повторное нажатие клавиши С/П приводит к появлению на индикаторе очередного случайного числа RAV.

Недостатком программы 1/34 является наличие в ней операторов условного перехода, что затрудняет ее использование в качестве подпрограммы, поскольку операторы 7 и 8 потребуют коррекции адреса перехода, если программа будет начинаться не с нулевого оператора.

Программа 2/34. Генерация псевдослучайных чисел с равномерным распределением в диапазоне (0...1)

	ИП9	Fp	+	Fe^x	П9	КИП9	XY	ИП9	-	П9
	С/П	БП

Инструкция: х_о=Р9; В/О; С/П; РХ = х₁, С/П; РХ == х₂.; С/П; РХ=х (время счета около 5с).

При X₀=0,5 получается множество случайных чисел Х={0,152545; 0,954155; 0,084227,...}. Программа занимает малый объем памяти и ее можно без редактирования фрагментарно вставлять в другие программы.

Для получения генератора k случайных чисел с равновероятными исходами, интервал (0..1) делится на k равных частей и организуется вывод на индикацию появления номера соответствующего подинтервала.

Программа 3/34. Генератор псевдослучайных событий с равномерными исходами.

	ИП9	Fp	+	Fe^x	П9	КИП9	XY	ИП9	-	П9
	ИП8	X		+	П7	КИП7	ИП7	С/П	БП

Инструкция: k=P8; x₀=Р9; В/О; С/П; РХ = y₁; С/П; РХ = у₂,..., С/П; РХ = у_n. В этой программе использована операция взятия целого от числа путем следующей подпрограммы

	П7	КИП7	ИП7	С/П	БП

Инструкция: х = РХ; В/О; С/П; Int(х)= Р(х). При статистических испытаниях сложных систем возникает потребность в получении случайной перестановки К чисел, имитирующих случайную последовательность отказов элементов. С этой целью можно использовать алгоритм «перемешивания» массива.

Программа 4/34. Перемешивание массива чисел.

	П0	ИПД	Fp	+	Fe^x	ПД	КИПД	XY	ИПД	-
	ПД	ИПС	Х		+	ПА	ИП0	ПВ	КИПВ	КИПА
	КПВ	XY	КПА	FLO		С/П

Инструкция: RАV=РД; x₁=Pl,...; x_k = PK; K=PC; k = РХ; В/О; С/П; PI = x₁,..., PK = x_k.

Дата добавления: 2015-10-16