Деление чисел в форме с плавающей запятой

Когда операнды заданы в форме с ПЗ: ,

то их частное определяется следующим образом:

,

т.е. мантисса частного есть частное от деления мантиссы делимого на мантиссу делителя, а порядок частного 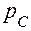есть разность порядков операндов. Это позволяет сформулировать алгоритм деления чисел в форме ПЗ.

1. Определить знак частного путем сложения по модулю два знаковых разрядов операндов.

2. Разделить модуль мантиссы делимого на модуль мантиссы делителя по правилам деления дробных чисел с ФЗ.

3. Определить порядок частного вычитанием порядка делителя из порядка делимого, используя при вычитании ОК или ДК.

4. Нормализовать мантиссу результата и присвоить знак, определенный в пункте 1 алгоритма.

В отличие от деления чисел в форме с ФЗ при делении чисел с ПЗ получение положительного остатка при первом вычитании не означает ПРС. Для чисел с ПЗ следует денормализовать мантиссу делимого сдвигом ее на один разряд вправо, увеличить на единицу порядок делимого и снова выполнить первое вычитание.

Однако, ситуация ПРС при делении чисел с ПЗ возможна при вычитании порядков операндов, если они были разных знаков.

Пример 12. Числа А=26₍₁₀₎ и В=-19₍₁₀₎ представить в форме с ПЗ в разрядной сетке условной машины и разделить, применив при делении модулей мантисс II способ с использованием ОК при вычитании и алгоритм деления без восстановления остатков.

А =11010(2)	Операнды в разрядной сетке условной машины
В =-10011(2)
	знак числа	Мантисса пять разрядов	знак порядка	Порядок четыре разряда

1. Знак частного: 0Å1=1.

2. Частное от деления модулей мантисс.

Таблица

Частное

  Делитель

Делимое (остатки)

Пояснения

0,1001100000

0,11010 00000 1,01100 11111

  1-е вычитание

10,00110 11111

0,00111 00000

1-й ост.>0 – признак ПРС!

Денормализация мантиссы делимого

А

0,1001100000

0,01101 00000 1,01100 11111

  Вычитание

0,0000 0

0,0100110000

1,11001 11111 1,11001 11111 0,01001 10000

1-й ост.<0 Сдвиги Сложение

10,00011 01111

  0,000 01

0,0010011000

0,00011 10000 0,00011 10000 1,11011 00111

2-й ост.>0 Сдвиги Вычитание

0,00 010

  0,0001001100

1,11110 10111 1,11110 10111 0,00010 01100

3-й ост.<0 Сдвиги Сложение

10,00001 00011

0,0 0101

0,0000100110

0,00001 00100 0,00001 00100 1,11110 11001

4-й ост.>0 Сдвиги Вычитание

0, 01010

  0,0000010011

1,11111 11101 1,11111 11101 0,00000 10011

5-й ост.<0 Сдвиги Сложение

10,00000 10000

0,10101

  0,0000001001

0,00000 10001 0,00000 10001 1,11111 10110

6-й ост.>0 Сдвиги Вычитание

10,00000 00111

0,10101 (1)

0,00000 01000

7-й ост.>0 Разряд для округления

Округление мантиссы частного:

0,10101

______1

0,10110

3.Вычитание порядков в ДК:

100001	-порядок частного.

3. Мантисса нормализована. Результат в разрядной сетке:

Проверка: -0,10110*2¹=-1,0110₍₂₎=-1,375_(10).

Точный результат: А/В=-(26/19)=-1,368₍₁₀₎; отн. погрешность = 0,51%.

Дата добавления: 2015-10-21