Вероятностные меры надежности СЭЭС

Мерой может быть положительное конечное вещественное число. Например, масса, стоимость, объем, число элементов множества, абсолютная температура и т. п. Меры обязательно должны обладать свойством аддитивности, т. е. мера множества будет равняться сумме мер его элементов.

Обозначим введение меры вектора Х через оператор m(..):

m (X) = m (x₁) + m (x₂) + m (x₃),

или в общем виде:

_m

m (X) = S m (x_i)

ⁱ⁼¹

Согласно общепризнанной аксиоматике, введенной А. Н. Колмогоровым, вероятность определяется как нормированная мера в фундаментальном пространстве состояний В и обладает следующими свойствами:

Если под P(x_i) понимать вероятность работоспособного состояния i-го элемента системы, а под Р(Х_j)—вероятность j-го состояния системы, то вероятность работоспособного состояния системы определится выражением

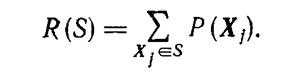
Если мерой эффективности электростанции является ее суммарная мощность, то она может быть вычислена для каждого состояния системы в кВт,

где x_i—целочисленный индикатор по (9) автоматически исключает из суммы мощность отказавшего агрегата.

Математическое ожидание эффективности электростанции можно оценить как сумму произведений мощности в i-м состоянии на вероятность этого состояния в области работоспособных состояний в кВт,

Если мерой эффективности ЭЭС является математическое ожидание выработанной ею энергии, то вероятности работоспособного состояния элементов должны задаваться как функции времени, например, при экспоненциальном законе распределения отказов

где l_i — интенсивность отказов i-го элемента системы.

Вероятность нахождения ЭЭС в одном из состояний (точке в пространстве состояние — время) определится произведением

где Q_i(t)=1—R_i(t)—вероятность отказа i-го элемента системы. Например, вероятность пребывания системы в состоянии x₅ (см. рис. 2) вычисляется по формуле

Математическое ожидание времени пребывания системы в данном состоянии за период наблюдения q определяется интегралом

Таким образом, можно оценить математическое ожидание наработки электрической энергии ЭЭС до первого отказа:

Если за q принять время нормальной работы (рис. 3.), то E будет соответствовать математическому ожиданию выработки электрической энергии за время “жизни” ЭЭС без учета восстановления.

В том случае, когда надежность ЭЭС определяют как комплексный показатель, включающий количественные оценки свойств C₁... С_п, возникает необходимость включения этих свойств в общую целевую функцию или ограничения. Чаще всего целевую функцию задают в аддитивной форме

где a_i — весовые коэффициенты.

Если свойство включается в состав ограничений, то оно приобретает свойства логической переменной, например

В этом случае свойство войдет в состав логических переменных, определяющих ФАЛ работоспособного состояния ЭЭС, например, в виде конъюнктивной формы

Если все свойства можно определить через вектор состояний ЭЭС, то ФАЛ работоспособного состояния по-прежнему будет задана на множестве В, т. е.

Рис. 4.

В ПРИЛОЖЕНИИ 1 приведены 34 варианта индивидуальных заданий для комплексной контрольной работы, содержащей основные разделы курса «теория надёжности». Ваш вариант задания должен совпадать с вашим порядковым номером в списке группы. Образец программы на языке MATHCAD для выполнения задания и ответы даны в этом же ПРИЛОЖЕНИИ 1.

Дата добавления: 2015-10-16