Глава 3. Проверка статистических гипотез

3.1. Проверка с помощью критерия согласия гипотезы о виде закона распределения СВ, уровень значимости α=0,05

Статистической гипотезой называется предположение о виде неизвестного распределения случайной величины или о параметрах известного распределения. Не располагая сведениями о всей генеральной совокупности, высказанную гипотезу сопоставляют, по определенным правилам, с выборочными сведениями и делают вывод о том, можно принять гипотезу или нет. Процедура сопоставления высказанной гипотезы с выборочными данными называется проверкой гипотезы.[См.1]

Располагая выборочными данными и руководствуясь конкретными условиями рассматриваемой задачи, формулируют гипотезу Н0, которую называют основной или нулевой, и гипотезу H1, конкурирующей с гипотезой Н0. Гипотезу Н1 называют также альтернативной.

Порядок проверки статистической гипотезы таков.

1. Располагая выборочными данными и руководствуясь конкретными условиями рассматриваемой задачи, формулируют основную гипотезу Н 0 и альтернативную гипотезу Н 1.

2. Выбирается статистический критерий 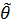_n.

3. По статистике 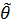_n и уровню значимости α определяется вид критической области. Для ее отыскания достаточно найти (обычно по таблицам для закона распределения 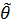_n) значение критической точки, т.е. границу, отделяющую критическую область от области принятия гипотезы.

Соблюдаем порядок проверки статистической гипотезы:

1. Выдвигаем основную гипотезу 𝐻0: случайная величина X подчиняется нормальному закону распределения.

2. Формулируем альтернативную гипотезу 𝐻1: случайная величина распределяется не по нормальному закону.

3.Рассчитываем критерий по формуле:

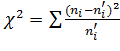(2.18)

4.Выбирается правосторонняя критическая область, и граница ее при заданном уровне значимости α и числом степеней свободы 𝑘 = 𝑣 − 1 − 𝑟, где v – число частичных интервалов выборки или вариант, r – число параметров предполагаемого распределения находится по таблице критических точек распределения 𝜒_кр² (𝛼,𝑘). Это значит, что если 𝜒2 <𝜒_кр² (𝛼,𝑘), то основная гипотеза принимается, в противном случае отвергается.

Произведя все действия по данному алгоритму(рисунок 12). Это говорит о том, что гипотеза о нормальном распределении принимается с ошибкой 0,05.

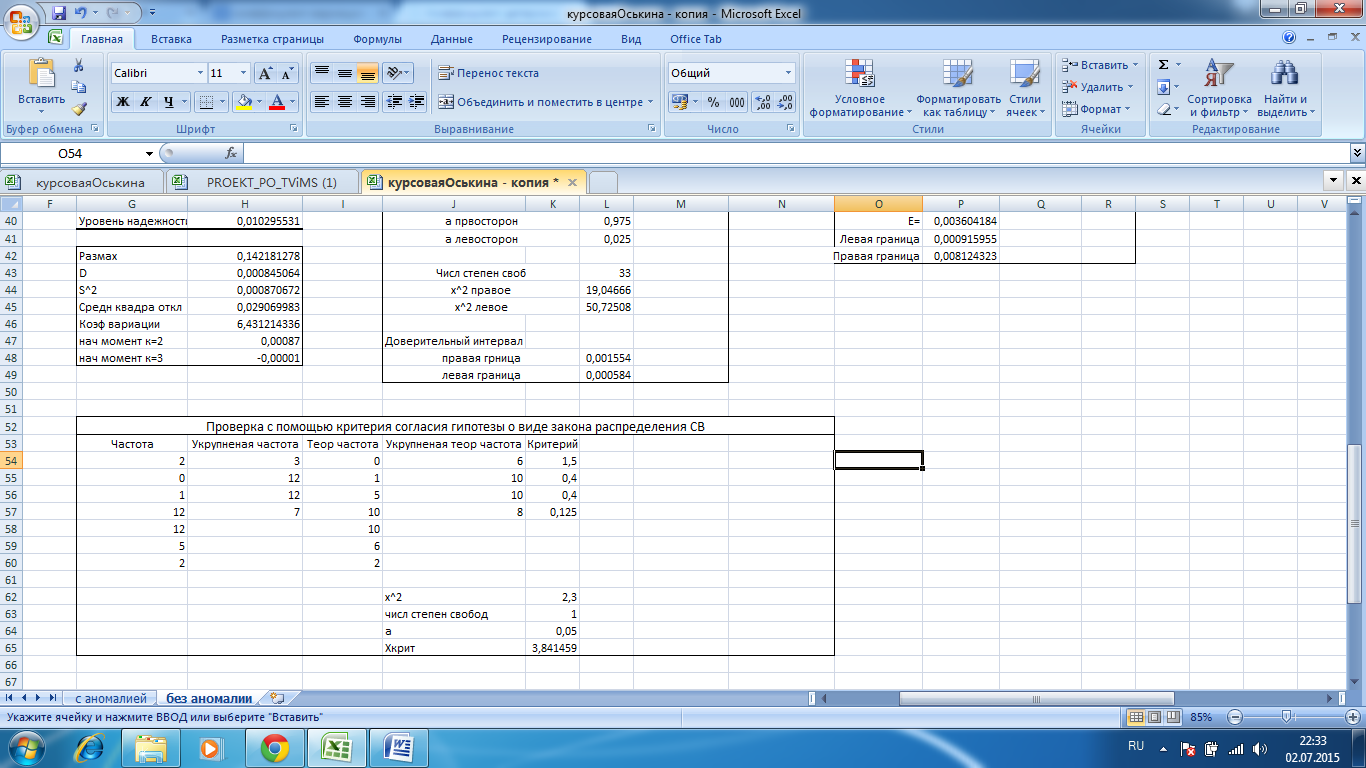
Рисунок 12 Проверка гипотезы о нормальном законе распределения

Дата добавления: 2015-10-16