Вычисление основных характеристик выборочных данных. Свойства полученных оценок.

Закон распределения случайной величины является исчерпывающей характеристикой, которая полностью описывает случайную величину с вероятностной точки зрения. Однако во многих практических задачах нет надобности в таком полном описании и достаточно указать только отдельные числовые параметры, характеризующие существенные черты распределения. Такие числа называются числовыми характеристиками случайной величины.

Основными характеристиками статистических данных являются математическое ожидание, мода, медиана, размах, дисперсия, среднеквадратическое отклонение, коэффициент вариации, начальный момент, эксцесс, ассиметрия.

Некоторые из них можно получить с помощью инструмента «Описательная статистика»»[См.3] (Рис.7)

Рисунок 7 Описательная статистка

Математическое ожидание характеризует среднее значение случайной величины и определяется по формулам:

(2.1)

где M[X] – оператор математического ожидания. Физический смысл математического ожидания – среднее значение случайной величины, т.е. то значение, которое может быть использовано вместо случайной величины в приблизительных расчетах или оценках. Математическое ожидание обладает следующими свойствами:

1. M[c] = c.

2. M[X + c] = M[X] + c = m_X + с.

3. M[c*X] = c*M[X] = c*m_X.

В данной выборке m_X = 0,001227023

Моду данная выборка не имеет.

Медиана случайной величины X равна такому ее значению, для которого выполняется условие p{X < Me} = p{X ≥ Me}. Медиана, как правило, существует только для непрерывных случайных величин. В данной выборке медиана равна 0,005696961.

Размах выборки это разность между максимальным и минимальным значениями переменной в наборе данных. Max = 0,06019, Min = -0,08198, размах = 0,14218.

Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и определяется по формуле:

(2.2)

Свойства дисперсии:

1. D[c] = 0.

2. D[X + c] = D_X

_3. D[c⋅X] = c²⋅D_X

В случае, если мы имеем дело не с генеральной совокупностью, а с выборкой, то вычисляется выборочная дисперсия:

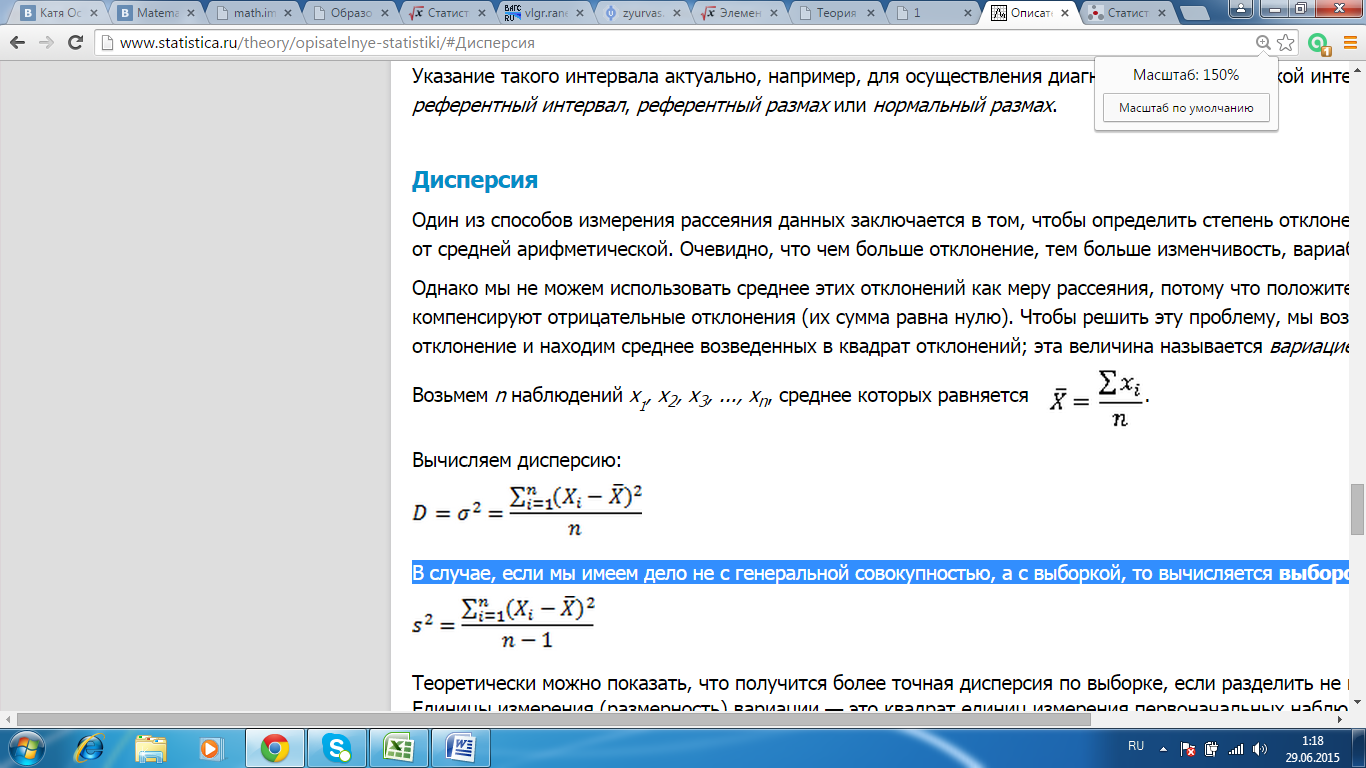_(2.3)

Для данной выборки D= 0,000845064, S² = 0,000870672.

Среднее квадратическое отклонение случайной величины X характеризует ширину диапазона значений X и равно:

σ _X = σ[x] = + . (2.4)

Для данной выборки σ _X = 0,029069983.

Стандартное отклонение выборки- среднее отклонение наблюдений от среднего. Оно вычисляется в тех же единицах (размерностях), что и исходные данные.

S = (2.5)

Для данной выборки S= 0,02950715.

Коэффициент вариации – мера рассеяния, не зависит от единиц измерения (безразмерный).

k = 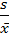(2.6)

Для данной выборки k = 6,431214336.

Начальный момент k-го порядка случайной величины X есть математическое ожидание k-й степени этой случайной величины.

(2.7)

Для данной выборки k = 0 a0(x) =1, k =1 a1(x) = m_X = 0,00087,k = 2 a2(x) =-0,00001.

Эксцесс – это количественная характеристика, выражающая меру остроты пика распределения случайной величины..

Эксцесс равен:

Ex= – 3 (2.8)

Для данной выборки Ex= 2,064265705.

Эксцесс для случайной величины, распределенной нормально, равен нулю. Поэтому за стандартное значение выборочного эксцесса принимают E = 0. В случае положительного эксцесса полигон более крутой по сравнению с нормальной кривой.

Выборочным коэффициентом асимметрии называется число , определяемое формулой:

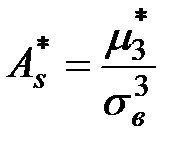. (2.9)

Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая. Если 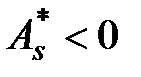, то более пологий «спуск» полигона наблюдается слева; если - справа. В первом случае асимметрию называют левосторонней, а во втором - правосторонней.

В данной выборке A_s^*= -0,862229168.

По данной выборке коэффициенты асимметрии и эксцесса не намного отличаются от нуля. Коэффициент асимметрии оказался отрицательным, что свидетельствует о левосторонней асимметрии данного распределения. Эксцесс оказался положительным. Это говорит о том, что кривая,которая изображает ряд распределения, по сравнению с нормальной имеет более крутую вершину. Все это дает возможность подтвердить гипотезу о том, что выборка курса доллар/рубль является нормальной.

Дата добавления: 2015-10-16