Построение доверительных интервалов для математического ожидания и дисперсии с надежностью 0,95.

Чтобы получить представление о точности и надежности оценки, используют интервальную оценку параметра. Вычисляют такую величину δ, которая с «практической достоверностью» (т.е. с заранее заданной вероятностью близкой к 1) гарантировала бы выполнение неравенства < δ. Т.е. выполнялось бы следующее

P ( < δ) = γ, (2.20)

или, что то же, находят интервал вида (), который с заранее заданной вероятностью (близкой к единице) накрывал бы неизвестное нам истинное значение искомого параметра. [См. 1]

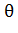P ( δ < < δ) = γ. (2.21)

При этом заранее выбираемая исследователем вероятность γ, близкая к единице, называется доверительной вероятностью или надежностью интервальной оценки.

Интервал () называется доверительным интервалом или интервальной оценкой характеристики θ. Число ε называется точностью оценки 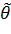или предельной ошибкой выборки, числа 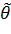и 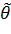называются доверительными границами. Надежность γ принято выбирать равной 0,95; 0,99; 0,999, мы будем работать с γ =0,95. Тогда событие, состоящее в том, что интервал () накроет характеристику θ, будет практически достоверным. Также практически достоверным является событие, состоящее в том, что погрешность оценки меньше δ, или, иначе, точность оценки больше δ.

Интервальная оценка дисперсии нормального распределения. Для построения интервальной оценки параметра воспользуемся тем фактом, что статистика подчинена - распределению с n-1 степенями свободы. Поэтому, определив из таблиц процентные точки - распределения с n-1 степенями свободы и , имеем неравенство

< . (2.22)

Разрешая это неравенство относительно , получаем, что случайный доверительный интервал (; ) накрывает неизвестное значение с заданной вероятностью γ.

Итак, построим доверительный интервал дисперсии для данной выборки. Значения и находятся при помощи функции ХИ2ОБР(), исходя из следующих условий:

(2.23)

(2.24)

Рисунок 9 Левое и правое хи-квадрат значения

Таким образом, получаем доверительный интервал для дисперсии, представленный на рисунке 10.

Рисунок 10 Доверительный интервал для дисперсии

Получили, что дисперсия выборки находится в интервале от 0,000584 до 0,001554.

Дисперсия отражает меру разброса данных вокруг средней величины, поэтому доверительный интервал показывает, что данные могут находиться в пределах найденного доверительного интервала.

Доверительный интервал для математического ожидания с надежностью 0,95.

Точность интервальной оценки для математического ожидания значения по формуле:

, (2.25)

где t находится с помощью функции НОРМОБР (вероятность; среднее; стандартное_откл).

Математическое ожидание выборки, которая имеет нормальный закон распределения, с доверительной вероятностью 1-a находится в доверительном интервале:

(2.26)

Итак, получаем доверительный интервал для математического ожидания рисунок 11.

Рисунок 11 Доверительный интервал для математического ожидания

Это значит, что математическое ожидание может находиться в пределах данного интервала при данном уровне надежности.

Дата добавления: 2015-10-16