Выявление грубых ошибок в статистических совокупностях. Исключение аномальных значений.

Методы робастного оценивания – это статистические методы, которые позволяют получать достаточно надежные оценки статистической совокупности.
Единицы статистической совокупности, у которых значения анализируемого признака существенно отклоняются от основного массива, называются аномальными явлениями, «грубыми ошибками» или выбросами.
При решении задач статистического анализа проблема наличия в выборке аномальных измерений имеет чрезвычайно важное значение. Присутствие единственного аномального наблюдения может приводить к оценкам, которые совершенно не согласуются с выборочными данными.

По полученным индексам построим график доходностей, на котором наглядно можно проследить аномалию курса рубля к доллару за данный период времени. (Рис. 4). В ходе визуального анализа выявляем наличие в выборке аномальных значений.

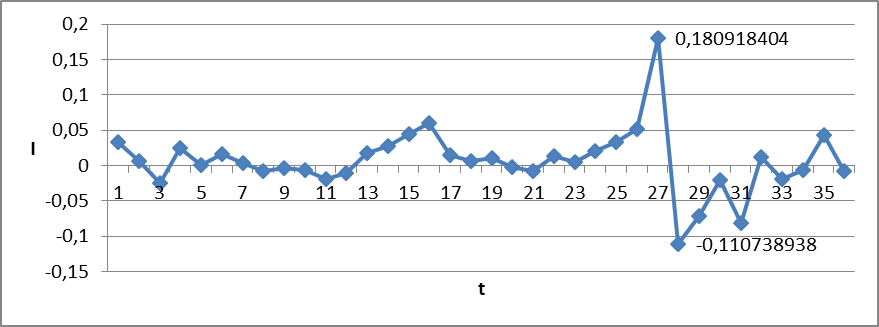
Рисунок 4 График доходностей

По графику видно, что аномалией является I = 0,180918, который произошел 16 декабря 2014 года и I = -0,11073894, который произошел 17 декабря 2014 года.

Простым способом для обнаружения грубых ошибок является Т – Критерий Граббса[См. 4]:

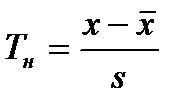, где (1.6)

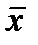- среднее значение;

x - аномальное значение;

s – Выборочное среднеквадратическое отклонение случайной величины.

Произведем расчеты по нашей выборке.(Табл.4)

Таблица 4 Расчет аномалии по критерию Граббса

Критерий Граббса(1)	Критерий Граббса(2)
х среднее	0,00621845	х среднее	0,00621845
s^2=	0,002086553	s^2=	0,002086553
s=	0,045678799	s=	0,045678799
Тк1=	3,82453039	Тк2=	2,560430468

Полученные значения 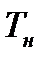для двух аномалий сравнивают с табличными значениями процентных точек критерия Смирнова Граббса (Табл.5). Если 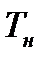> 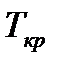, то проверяемое значение является грубой ошибкой и относится к классу выбросов.

Таблица 5 Значения процентных точек критерия Смирнова Граббса

n	Доверительная вероятность (1-а)	n	Доверительная вероятность (1-а)
0,9	0,95	0,99	0,9	0,95	0,99
	1,412	1,414	1,414		2,749	2,913	3,239
	1,689	1,710	1,728		2,764	2,929	3,258
	1,869	1,917	1,972		2,778	2,944	3,275
	1,996	2,067	2,161		2,792	2,958	3,291
	2,093	2,182	2,310		2,805	2,972	3,307
	2,172	2,273	2,431		2,818	2,985	3,322
	2,238	2,349	2,532		2,830	2,998	3,337
	2,294	2,414	2,616		2,842	3,010	3,351
	2,343	2,470	2,689		2,853	3,022	3,364
	2,387	2,519	2,753		2,864	3,044	3,377
	2,426	2,563	2,809		2,874	3,055	3,389
	2,461	2,602	2,859		2,885	3,064	3,401
	2,494	2,638	2,905		2,894	3,065	3,413

Т.к. Т_к1 =3,82453, Т_к2 = 2,56043, 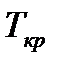= 3,377 (с доверительной вероятностью 0,01), и Т_к1 > 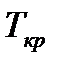следовательно проверяемое значение является грубой ошибкой и относится к классу выбросов, однако Т_к2 не удовлетворяет данному условию.

Критерий Граббса имеет некоторые недостатки. Он не точен, и не чувствителен к засорениям, когда ошибки группируются на расстоянии от общей совокупности.

По сравнению с оценками Граббса оценками грубых ошибок признаются L- и E- критерии, предложенные американскими статистиками Г. Тритьеном. И Г.Муром. [См. 4]:

L-Критерий применяется для вычисления грубых ошибок:

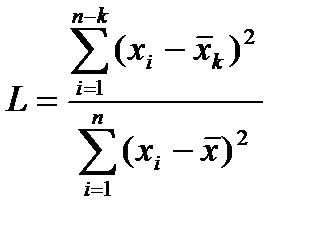, где (1.7)

где 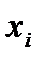- выборка наблюдений;

n – объем выборки;

k – число наблюдений с резко отклоняющимися значениями признака;

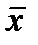- общая для выборочной совокупности данных средняя величина;

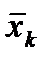- средняя, которую рассчитывают по n – k наблюдениям, остающимися после отбрасывания k грубых ошибок ранжированного ряда данных:

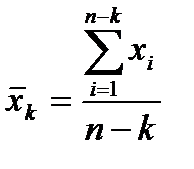(1.8)

Если наблюдаемые значения критериев оказываются меньше пороговых, то ошибки в данных, признаются грубыми.

Произведем расчеты по нашей выборке.(Табл.6)

Таблица 6 Расчет L- критерия Титьена-Мура

x cpеднее	0,00621845	x cpеднее без k	0,004520139
Сумма:	0,073029343	Сумма:	0,028732174
L=	0,393433275

Сравним наблюдаемые значения критериев с пороговыми(Табл.7)

Таблица 7 Критические значения оценки для L - критерия Титьена и Мура (a=0,05)

Т.к. L_к =0,39343, L_kp= 0,762, L_к < L_kp то проверяемое значение является грубой ошибкой и относится к классу выбросов. В проверке участвовали 2 предполагаемых аномальных значения и оба подтвердили, что они аномальны.

Таким образом, на основании Т – критерия Граббса и L - критерия Титьена-Мура мы подтвердили, что выявленное в ходе визуального анализа аномальные явления являются таковыми. Индекс первого аномального значения I=0,180918, значение его выборки х = 72,5, дата его выброса 16 декабря 2014 года, индекс второго аномального значения I= -0,11073, значение его выборки х = 64,9, дата его выброса 17 декабря 2014 года.
Исключая аномальное значение, по формулам(1.2,1.3,1.4,1.5) определим минимум выборки без аномалии, максимум, шаг и количество интервалов. (Табл.8).Получаем выборку без аномалий(Табл.9).

Таблица 8

Минимум	-0,08198
Максимум	0,06019
Кол-во интервалов	5,93690
Шаг	0,023948

Таблица 9 Выборка без аномального значения

<DATE>	Выборка	Ряд доходностей
05.11.2014	44,52750
06.11.2014	46,00000	0,032534421
07.11.2014	46,29950	0,006489765
10.11.2014	45,15000	-0,025140882
12.11.2014	46,30000	0,025151681
13.11.2014	46,35600	0,001208772
14.11.2014	47,10000	0,015922268
17.11.2014	47,23050	0,002766869
18.11.2014	46,86050	-0,007864767
19.11.2014	46,70000	-0,003430938
20.11.2014	46,39000	-0,006660246
21.11.2014	45,48000	-0,01981125
24.11.2014	44,99450	-0,010732409
25.11.2014	45,79900	0,017721997
26.11.2014	47,05000	0,026948609
28.11.2014	49,20000	0,044682757
01.12.2014	52,25250	0,060194113
02.12.2014	53,00000	0,014204177
03.12.2014	53,33700	0,006338361
04.12.2014	53,90000	0,010500204
05.12.2014	53,81000	-0,001671154
08.12.2014	53,42000	-0,007274116
09.12.2014	54,15950	0,013748189
10.12.2014	54,43400	0,005055562
11.12.2014	55,57000	0,020654529
12.12.2014	57,48000	0,033793574
15.12.2014	60,50150	0,051231097
18.12.2014	60,45000	-0,071031047
19.12.2014	59,20000	-0,020895035
22.12.2014	54,54000	-0,081987164
23.12.2014	55,20000	0,012028576
24.12.2014	54,13000	-0,019574392
26.12.2014	53,80050	-0,0061058
29.12.2014	56,17000	0,043100046
30.12.2014	55,69950	-0,008411636

Построим интервальный статистический ряд.(Табл.10)

Таблица 10

Карман	Частота
-0,093961525
-0,070012804
-0,046064082
-0,022115361
0,00183336
0,025782082
0,049730803
0,073679525

И гистограмму выборки без аномалии(Рис.5)

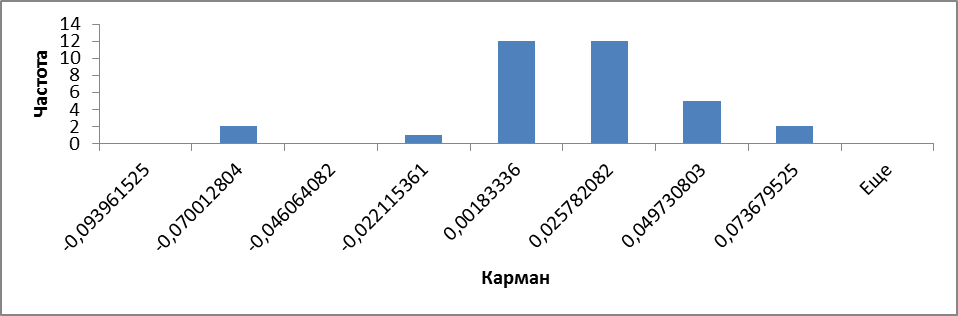
Рисунок 5 Данные без аномального значения

Дата добавления: 2015-10-16