Точечные оценки параметров предполагаемого закона распределения случайных величин методом максимального правдоподобия.

Метод максимального правдоподобия — еще один разумный способ построения оценки неизвестного параметра. Состоит он в том, что в качестве «наиболее правдоподобного» значения параметра берут значение θ, максимизирующее вероятность получить при n опытах данную выборку X={X₁,…X_n}. Это значение параметра θ зависит от выборки и является искомой оценкой.[См. 6]

Пусть случайная величина x ∈ N (a, σ), θ = (a, σ) - оцениваемые параметры распределения.

Выпишем плотность, функцию правдоподобия и логарифмическую функцию правдоподобия.

Плотность:

(2.10)

Функция правдоподобия:

L(a, σ) = (2.11)

Тогда логарифмическая функция правдоподобия:

ln L(a,σ) = -n*ln σ -n*ln - (2.12)

Условия экстремума:

(2.13)

(2.14)

Получили систему:

(2.15)

(2.16)

(2.17)

Корни этой системы уравнений:

, (2.18)

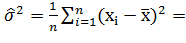D. (2.19)

Таким образом, в качестве оценки получаем: для среднего a нормального закона - выборочное среднее, а для дисперсии - выборочную дисперсию D.

Дата добавления: 2015-10-16