Оценка помехоустойчивости. Распределение на входе устройства сравнения будет Райса и Релея.

Распределение на входе устройства сравнения будет Райса и Релея.

Алгоритм приемника прост: если огибающая в одном канале больше, чем в другом, то принимается решение о принятии этого значения.

Используется сигнал с активной паузой. Можно утверждать, что ошибка будет, когда

(1) - вероятность ошибки

Апостриорные вероятности

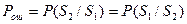- вследствие симметрии схемы

Огибающая шума: - распределение Релея

P(S2/S1)=P(Uш>Uсш) = 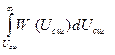(сш = с+ш)

Можно ли по выражению (1) осуществить расчет вероятности ошибки?

Принципиально нельзя, так как нижний придел интегрирования - случайная величина.

Нужно знать распределение случайной величины - это распределение Райса

Приближенно 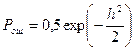(1)

-

мощность сигнала

-отношение на входе IPC

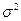-мощность шума

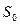- амплитуда шума

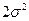- отношение сигнал/шум на выходе идеального оптимального приемника

- полоса=1

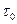-длительность

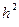= на выходе коррелятора, на входе IPC

- база

Сравнение выражения(2) с выражением для вероятности ошибки идеального оптимального приема частотноманипулированных сигналов: , показывает, что для диапазона вероятности ошибки 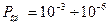приемник имеет энергетический проигрыщ 30-15%.

Эти расчетные соотношения показывают, что есть серьезная конкретная проблема: при хороших отношениях сигнал/шум, некогерентный приемник работает хорошо, проигрыш меньше 15%.

При достаточно плохих отношениях сигнал/шум, нужно использовать интеграл вероятности, а не экспоненциальную форму. Проигрыш некогерентного приема сильно возрастает, следовательно, нужно добавить избыточность.

При приличных отношениях SNR, когда обеспечивается вероятность ошибки 10^-6 и лучше эта двухканальная схема работает достаточно хорошо.

Можно в качестве полосовых фильтров использовать активные следящие фильтры.

Дата добавления: 2015-09-06