Оценка помехоустойчивости.

В решаемом устройстве должен быть выбран порог(принятия 0 и 1)

Смесь сигнала и шума меньше порогового

Принимается шум

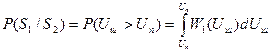
Распределение смеси сигнала и шума называется распределением Райса:

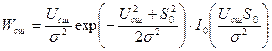
где - функция Бесселя нулевого порядка первого рода.

- амплитуда полезного сигнала

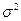- дисперсия, мощность помехи(гауссов шум)

Функция распределения огибающей шума подчиняется распределению Релея:

Для бинарной связи необходимо, чтобы

(*)

Для выполнения этого условия необходим выбор оптимального порога. Эта задача решается сложными методами (методами вариационного вычисления). Оказывается, что этот порог должен изменяться в зависимости от отношения сигнал/шум.

Отношение сигнал/шум на входе это:

Для простых сигналов, приблизительно можно считать, что (на входе и на выходе РС). И для выполнения условия(*) оптимальное значение порога должно изменяться с отношением сигнал/шум следующим образом:

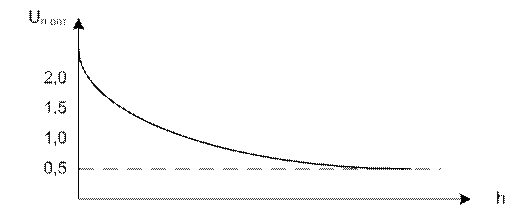
Таким образом приближенное вычисление для

(1)

Для оптимального приема сигналов с пассивной паузой: (2)

Сравнение выражений по помехоустойчивости . Некогерентный прием требует увеличения энергии сигнала на 30-15% по сравнению с оптимальным чисто когерентным приемом.

В реальной схеме передачи информации на входе решающего устройства не будет принципиально гауссовского распределения. А будет распределение либо Райса, либо Релея, вследствие ограниченности сигнала на входе

С увеличением мощности шума, а следовательно дисперсионных характеристик распределения Релея и Райса, это различие между вероятностями ошибки для приема 1 и 0 при фиксированном пороге будет возрастать.

Если отношение сигнал/шум хорошее, то можно работать с фиксированным порогом, например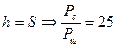

Как только мы начинаем работать с плохими отношениями сигнал/шум, необходимо регулировать порог, следовательно появляется задача оценки состояния канала связи(в хорошей схеме оценка должна быть постоянно).

Например: Какие есть возможности для оценки:

1. Когда используется корректирующая коды информация об обнаруженных ошибках во многом определяет состояние канала связи
2. Огибающая на сигнале на входе расчетной схемы также во многом определяет отношение сигнал/шум

Для идеального оптимального приемника сигнал на выходе коррелятора (согласованного фильтра) является фактическим отношением сигнал/шум.

Дата добавления: 2015-09-06