Оптимальное различение дискретных сигналов методом проверки статистических гипотез.

Постановка задачи: метод был разработан для обработки результатов физических экспериментов. Затем был успешно применен для анализа помехоустойчивости, радиолокации.

Нужно придумать правило, по которому будем принимать решение, какой сигнал принят. Тогда у нас будет алгоритм, на основе которого можно построить приемник. Затем придется оценить его помехоустойчивость.

При приеме двоичных сигналов необходимо получить наилучший метод приема обработки сигналов. Фактически приемное устройство должно решить задачу, какой сигнал принят: или .

Такая задача является задачей выбора двух гипотез: 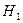или

Она статистическая, так как в общем случае появление сигнала и - случайный процесс.

Правила. Принят сигнал s2. На этой основе просто записать:

передан	Выбор гипотезы
верна	ошибочна
S1(t)	H1 - верно	H2 - ошибка
S2(t)	H1 - ошибка	H2 - верно

Тут тривиально. На этой основе можно строить более сложный случай.

Перед нами стоит задача разработки критерия (правила), которое должно привести к самому лучшему оптимальному приемнику.

Исходя из здравого смысла. Решение должно быть принято на основе анализа случайного колебания y(t)=S_i(t)+n_j(t)

В результате анализа мы должны получить апостриорную вероятность:

Мораль такая: если (какая вероятность больше, такой сигнал и принят)

Серьезные выводы: для принятия решения необходимо осуществить оенку апостриорных (после опыта) вероятностей. Т.е. мы считаем, что это условие самое правильное и самое хорошее.

Это и есть наш постулат. Дальнейшее его преобразование – его модификация.

Ввести отношение правдоподобия (простая трансформация):

Это и есть наш исходный постулат.

Воспользуемся формулой Байеса.

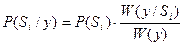
- априорная вероятность появления сигнала

- функция (многомерная или условная) плотности распределения входного колебания y(t) при фиксированном для данного значения на входе сигнала .

- многомерная безусловная функция распределения колебания y(t)

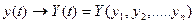
Справедливо для так называемого эргодического стационарного процесса (осреднение по времени заменяется осреднением по ансамблю – свойство эргодичности).

Если воспользоваться формулой Байеса, то отношение правдоподобия можно преобразовать.

При условии, что на входе действует помеха типа белого гауссовского шума, то есть y-гауссовский процесс, то распределение имеет вид:

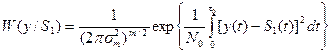
m – размерность.

дисперсия шума или мощность шума в некоторой полосе

- для гауссовского шума.

Подставляем в отношения правдоподобия и получаем:

(1)

Получим решающее правило

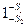
Для реализации оптимального приемника необходимо иметь образец.(1)

Пределы интегрирования необходимо проводить от 0 до (то есть иметь синхронизацию - знать временные пределы)

Дата добавления: 2015-09-06