Вероятность ошибки при оптимальной приеме двоичных сигналов с пассивной паузой или помехоустойчивость приемников сигналов с пассивной паузой.

Читайте также:

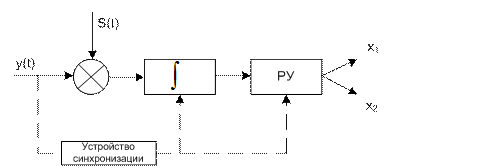
n(t) – гауссовский шум с постоянной 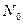спектральной плотности.

Возможны 2 случая:

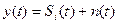
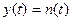
Мощность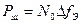

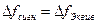
Таким образом, на выходе имеем 2 варианта в соответствии с решающим правилом.

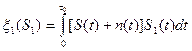
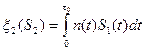
Решающее устройство имеет порог q=E/2 (вследствие решающего правила)

Решающее правило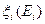

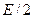
Вероятность правильного приема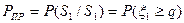

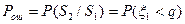
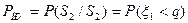
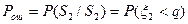
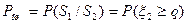
Характеристики распределения: Математическое ожидание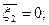

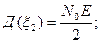
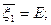
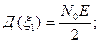
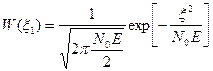
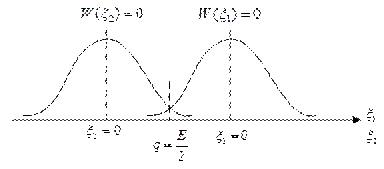
Изобразим функцию распределения графически:

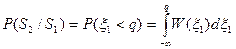
Вероятность ошибки в приеме сигнала

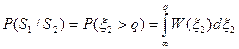
Это является доказательством того, что вероятности приема 0 и 1 равны.

Площади их хвостиков равны, потому что дисперсии одинаковые. Дисперсия зависит от отношения сигнал/шум и если это требование не соблюдается, то возникает очень серьезная задача.

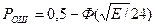
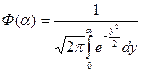- функция Лапласа (часто называют интегралом вероятности)

Или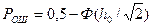

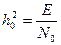- отношение сигнал/шум на выходы коррелятора

Дата добавления: 2015-09-06; просмотров: 171 | Нарушение авторских прав

Читайте в этой же книге: Зависимость погонной индуктивности. | Организация каналов связи на линиях электропередач. | Аддитивно-мультипликативная модель | Оценка состояния канала связи (оценка помеховой обстановки) | Синусоидальные индустриальные помехи | Основные предпосылки | Ошибки dt по тактовой синхронизации, ошибки по фазе приводят к снижению SNR. | Оптимальное различение дискретных сигналов методом проверки статистических гипотез. | Структура оптимального приемника на фоне белого гауссовского шума. | Реализация оптимального приемника на основе согласованного фильтра |

<== предыдущая страница	\|	следующая страница ==>
Оптимальный приемник двоичных сигналов с активной паузой	\|	Вероятность ошибки при приеме двоичных сигналов с активной паузой или помехоустойчивость приемника сигналов с активной паузой.

mybiblioteka.su - 2015-2024 год. (0.008 сек.)