Базы сигналов

Изобразим энергию сигнала следующим образом:

Отношение сигнал/шум на выходе коррелятора на входе решающей схемы:

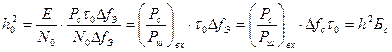
Чаще всего =полоса сигнала

-длительность информативного символа

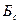-база сигнала

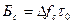
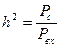
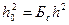
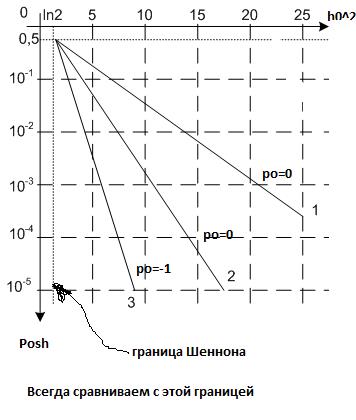
Первая кривая характеризует сигналы с пассивной паузой (коэф корреляции = 0)

Вторая – с активной паузой. Помехоустойчивость выше, чем у сигналов с пассивной паузой.

Третья – противоположные сигналы. ФМ (pi). Помехоустойчивость максимальна.

Если у стационарной помехи есть эффект нормализации, то её можно считать гауссовской.

Эти кривые для сравнения со своими результатми. Они не должны отличаться на порядки.

Простой сигнал

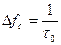
Если 1 бит передается за (длительность бита совпадает с длительностью информационного сигнала), то сигнал простой и 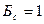. В этом случае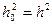

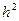- SNR на входе.

Для простого сигнала и оптимального приемника они равны (на выходе и на входе).

Т.е. SNR не должно ухудшаться.

Замечание:

При линейной обработки сигналов изменение SNR не происходит!

(например, линейный усилитель – полоса согласована с полосой сигнала(не вносит частотных искажений; не искажает ни частоты ни фазы сигнала)

Это фундаментальный вывод в обработки информации.

Совершенно понятно, что базу можно сделать равной 1. Это возможно, если:

• увеличить полосу.
• увеличить частотные затраты

Если 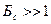, то это сложные, шумоподобные сигналы. Для таких (напр беспроводные локальные сети около 3, для косимческих – сотни и тысячи)

Таким образом, длина М-последовательности M=2^n - 1

Используют матрицу

Для таких сигналов с Б>>1:

• Позволяют повысить SNR на выходе
• Позволяют располагать весьма низким SNR на входе
• Если грамотно построить систему сигналов, то они будут почти ортогональны (обладают хорошими корреляционными свойствами)

Кроме М-последовательностей применяются и другие ортогональные коды. Когда-то в космических системах сигнал мог быть в тысячи раз ниже шума(!)

Прием сигнала в таких условиях осуществлялся достаточно долго. Можно позволить иметь низкую энергетику радиолинии. Как особенность систем с М-последовательностями.

Сама она достаточно хитрая вещь. Бывает сложно разпознать\перехватить сам факт передачи – определить образующий полино.

В теории кодирования доказали, что если знаешь 2n символов, то можно определить образующий полином (с линейной последовательностью).

Все это дается ценой скорости!

Можем варьировать число регистров сдвига. В длине мы вообще не ограничены, как и по образующему полиному. Вобщем, тема что надо.

Таким образом, для сигналов с базой больше единицы в помехоустойчивости мы можем уйти сюда:

Это совершенно эквивалентно избыточному кодированию. Оно, фактически улучшает SNR.

А как для простых сигналов? Это структурная избыточность. Если в приемнике организовать n независимых (с точки зрения воздействия шумов) копий одного сигнала одной и той же информационной последовательности, то можно теоретически неограниченно повышать помехоустойчивость приема простых сигналов с базой, равной единице. Тогда уже будет несколько передатчиков (частотное разнесение).

Способ, близкий к информационной избыточности – это повторение.

Распространено пространственное разнесение.

Сейчас эта структурная избыточность приобретает все более и более практический характер. Если можно построить многоканальную систему, то достоверность и скорость обработки информации можно в разы повысить.

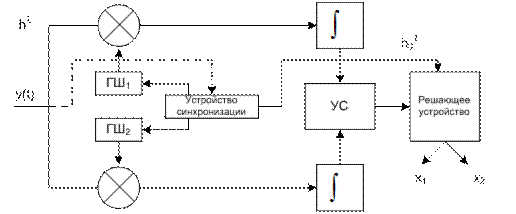
ГШ – генератор шума.

Прямая физическая реализация этой схемы стала неудовлетворительной, следовательно стали применять псевдослучайные последовательности Хаффмана вместо генератора шума.

Дата добавления: 2015-09-06