Рівняння руху ланки зведення

Аналітична залежність між діючими на ланки навантаженнями і кінематичними параметрами руху називається рівнянням руху. Після визначення характеристик (3.1) і (3.2) складається рівняння руху ланки зведення у енергетичної або диференціальної формі. Закон, одержаний при розв’язанні рівняння руху ланки зведення, співпадає із законом руху вхідної ланки.

Запишемо рівняння зміни кінетичної енергії ланки зведення в довільному інтервалі часу : , де 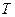– поточне значення кінетичної енергії; – значення кінетичної енергії на початку інтервалу; 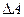– повна робота зведених навантажень; – робота зведених рушійних навантажень; 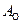– робота зведених навантажень опору. Значення усіх чинників рівняння ланки зведення мають наступний вигляд: ; ; 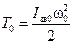; 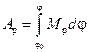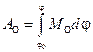, де і – значення зведеного моменту інерції та кутової швидкості на початок розглянутого проміжку часу.

З урахуванням вказаних залежностей, рівняння руху ланки зведення в енергетичної формі набуває наступного вигляду

. (3.3)

З рівняння (3.3) отримаємо залежність для визначення кутової швидкості ланки зведення

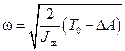(3.4)

Отримана залежність має неявний вигляд, оскільки обидві частини рівняння залежать від узагальненої координати 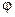, що не дає можливості отримати аналітичне розв’язання рівняння (3.3). Закон руху вхідної ланки 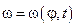на підставі рівняння (3.3) визначається графоаналітичними методами.

Рівняння руху ланки зведення у диференціальної формі має вигляд

. (3.5)

Рівняння (3.5) у загальному випадку є нелінійним диференціальним рівнянням, розв’язання якого може бути виконаним тільки наближеними методами. Рішення для окремих випадків наведені у навчальної літературі, наприклад у посібнику [4].

Дата добавления: 2015-10-13