Приклад 2.1.

Визначити передаточне відношення планетарної передачі з мішаним зачепленням сателітів (рис. 2.3, в) при наступних числах зубів: 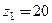; ; ; 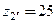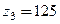. Ведучою ланкою вважати сонячне колесо 1.

Розв’язок

Передаточне відношення планетарної передачі визначається згідно (2.5).

Для наданої схеми обернений механізм має вигляд двохступінчастої співвісної передачі(рис. 2.3,а). Передаточне відношення оберненого механізму розраховується як для звичайного механізму з нерухомими паралельними осями, тобто

.

Після підстановки у формулу (2.5), знайдемо розрахункову залежність і визначимо результат за наданими вихідними

.

Відповідь: .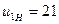

Умови синтезу планетарних передач

При проектуванні планетарних передач с заданим передаточним числом виникає необхідність розв’язання задачі підбору чисел зубів з урахуванням наступних умов:

1) кінематична умова;

2) умова співвісності вхідного і вихідного валів передачі;

3) умова сусідства сателітів;

4) умова складання;

5) умови правильного зачеплення при внутрішньому або зовнішньому контакті коліс.

Фізичне та математичне значення цих умов розглянемо на конкретних схемах планетарних передач з нульовими евольвентними циліндричними колесами (рис. 2.4).

а)	б)
в)	г)
Рис.2.4. Кінематичні схеми планетарних редукторів: а) Давида – із зовнішнім зачепленням сателітів; б) із змішаним зачепленням сателітів; в) Джемса; г) Давида – із внутрішнім зачепленням сателітів

За кінематичною умовою необхідно забезпечити дотримання передаточного відношення з відхиленням від розрахункового значення у припустимих межах. Теоретичні значення для найпоширеніших кінематичних схем планетарних передач розраховуються за формулами, наведеними у табл. 2.1. При проектуванні дозволяється відхилення від заданих або розрахункових значень на 2¼5%.

Співвісність центральних коліс і водила визначає розташування всіх центральних коліс і водила на загальній осі. Ця умова може бути визначеною через співвідношення розмірів або чисел зубів коліс (табл. 2.1).

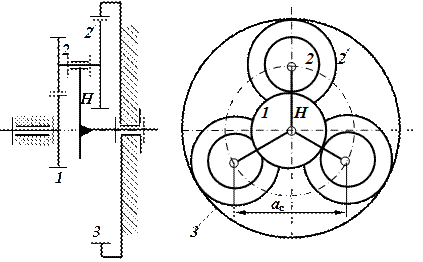
Рис.2.5. Редуктор зі змішаним зачепленням сателітів у двох проекціях

Умова сусідства визначає можливість спільного розміщення декількох сателітів по загальному колу таким чином, щоб сусідні сателіти не торкались один одного. Необхідність виконання цієї умови виникає при кількості сателітів . Зростання кількості осей сателітів зменшує навантаження на зубці, але ускладнює умови складання. Рівномірне розташування осей забезпечує зрівноважування механізму при рівномірному розподілі навантаження по зонах зачеплення. Максимально можлива кількість рухомих осей визначається з умови відсутності контакту між сусідніми сателітами (рис. 2.5). У передачах з рухомими осями, залежно від кінематичної схеми механізму, сателіти встановлюються на осях водила по одному або по двох на кожній осі. Для забезпечення відсутності контакту між сусідніми сателітами необхідно, щоб міжосьова відстань перевищувала подвійний радіус кола вершин найбільшого з сателітів, тобто . Для цієї схеми з нульовими евольвентними циліндричними колесами міжосьова відстань визначається залежністю , а радіус 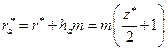, то умова сусідства набуває вигляду . З цієї нерівності визначається максимальне припустиме значення кількості рухомих осей сателітів

.

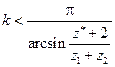При використанні градусної шкали кутів відповідні залежності до визначення кількості рухомих осей сателітів наведені у табл. 2.1.

Умова складання визначає рівні центральні кути між сателітами і враховує необхідність одночасного зачеплення усіх сателітів с центральними колесами. Після установки першого сателіту, кінематичний ланцюг замикається. Це означає, що після повороту водила центральне колесо приймає строго певне положення, і, якщо не виконати деяких вимог, то при установці наступних сателітів їхні зуби можуть і не виявитися точно проти западин центральних коліс. Тоді здійснити складання механізму неможливо. Щоб цього уникнути, необхідно так підібрати числа зубів коліс, щоб зуби всіх сателітів точно входили в западини центральних коліс. Співвідношення між числами зубів і кількістю осей сателітів 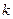наведені у табл. 2.1.

Таблиця 2.1. Умови підбора чисел зубів планетарних механізмів

Схема планетарного механізму	Передаточне відношення	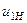Умова співвісності	Кількість рухомих осей сателітів	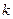Умова складання
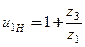
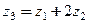
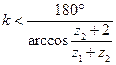
Джемса (рис. 2.4,)				, де C – будь-яке ціле число
зі змішаним зачепленням сателітів (рис.2.3, в)			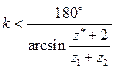де z ^* – більше із чисел зубів z 2 і	, де C – будь-яке ціле число, p – також ціле число. Воно представляє собою число повних монтажних обертів водила при установці кожного наступного сателіта.
Давида, із зовнішнім зачепленням сателітів (рис. 2.3, г)
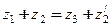
Давида, із внутрішнім зачепленням сателітів (рис. 2.3, г)

Умови правильного зачеплення включають умову відсутності підрізу зубів у коліс із зовнішнім зачепленням і умову відсутності заїдання (інтерференції) у внутрішньому зачепленні.

Підріз ніжки зуба більшого колеса виникає при контакті профілів зубів за межами теоретичної лінії зачеплення. У подібному контакті замість торкання евольвентні профілі перетинаються. Коренева частина зуба більшого колеса підріжеться. У зовнішніх зачепленнях мінімальне число зубів меншого з коліс повинне задовольняти умові відсутності підрізу, за якою . Для прямозубого нормального зачеплення: кут нахилу зуба ; кут зачеплення ; коефіцієнт висоти головки зуба 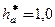; коефіцієнт зсуву . Мінімальне число зубів у нормальному зачепленні .

Відсутність інтерференції зубів при внутрішнім зачепленні коліс. Ця умова визначає відсутність заклинювання передачі. При внутрішнім зачепленні зубчастих коліс небезпечним стає явище інтерференції зубів. При цьому головка зуба малого колеса вдавлюється у голівку зуба більшого колеса за межами області зачеплення. Припустимі комбінації чисел зубів, що визначають умову відсутності інтерференції, наведені у табл. 2.2.

Таблиця 2.2. Умови відсутності інтерференції зубів при внутрішнім зачепленні коліс 2 і 3 (рис.2.1)

z 2

27..79

80 і вище

z 3

µ

>144

>81

>60

>50

>44

>41

>38

>36

>35

> +8

> +7

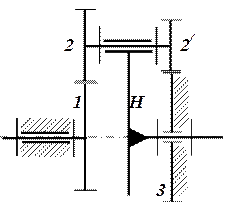
Приклад 2.2. Кінематичне дослідження механізму передачі

Механізм передачі (рис.2) складається з послідовно з`єднаних між собою електродвигуна М, планетарного редуктора та відкритої передачі. За вихідними даними необхідно визначити:

a) загальне передаточне відношення від електродвигуна до кривошипа (рис.1,в);

b) невідоме число зубів планетарного редуктора, використовуючи умову співвісності;

c) передаточне відношення планетарного редуктора;

d) передаточне відношення 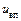відкритої передачі.

Підібрати числа зубів , , виходячи з умови відсутності підрізу меншого колеса. Прийнявши або , заокруглити отримане число зубів 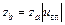до найближчого цілого числа таким чином, щоб відхилення 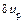нового значення передаточного числа 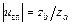відкритої передачі не відрізнялось від розрахункового більш, ніж на 4%.

Вихідні дані: Частота обертання кривошипа 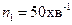; Частота обертання вала двигуна ; Числа зубів планетарного редуктора ; ; .

Рис. 2. Передаточний механізм

1. Розрахунок загального передаточного відношення

Загальне передаточне відношення розраховується за відомою формулою:

.

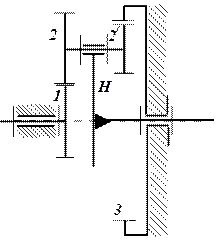
2. Визначення невідомого числа зубів z₃ планетарного редуктора.

До складу планетарного редуктора (рис. в) входять зубчасті колеса 1, 2, 2¢, 3 та водила H. Однієї з умов забезпечення його роботоздібності є умова співвісності z₁ +z₂ = z₃-z₂ ¢, з якої можна визначити невідоме число зубів:

z₃ = z₁ + z₂ + z₂¢ = 20+80+25 = 125.

3. Розрахунок передаточного відношення планетарного редуктора.

Передаточне відношення планетарного редуктора з мішаним зачепленням сателітів розраховується за формулою Віліса .

4. Розрахунок передаточного відношення відкритої передачі та підбір чисел зубів z_а, z _b.

Оскільки загальне передаточне відношення u = u_1H ×u_вп, тому з цієї формули знайдемо передаточне відношення відкритої передачі .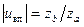

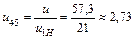Виходячи з умови відсутності підрізу зубів z_min >17 приймаємо число зубів для меншого з коліс z_а =18, тоді число зубів більшого колеса z _b = z _a ×u₄₅ = 18×2,73 = 48,6. Приймаємо z ₅ = 49. За цими числами зубів передатне число відкритої передачі 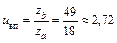незначно відрізняється від розрахункового значення, що є припустимим.

Питання для самоконтролю

1. Назвіть основні методи виготовлення зубчастих коліс. Вкажіть їх переваги і недоліки.

2. Як відбувається нарізання зубів методом обкочування?

3. Чому евольвентне зубчасте зачеплення має переважне застосування?

4. Які параметри визначають геометрію вихідного контуру?

5. Що таке коефіцієнт зміщення інструментальної рейки?

6. В чому полягає явище підрізування зуба при виготовленні зубчастих коліс?

7. Яке зміщення називають додатним, а яке – від'ємним?

8. Які колеса називають нульовими, додатними і від'ємними? Їх основні відмінності.

9. Як змінюється товщина зуба в залежності від величини зміщення інструментальної рейки?.

10. В яких випадках виконують коригування зубчастих коліс?

11. Як впливає зміщення інструментальної рейки на діаметр кола вершин і висоту голівки зуба зубчастого колеса?

12. При якому зміщенні інструментальної рейки можна нарізати зубчасте колесо з числом зубів меншим, ніж мінімально допустиме?

13. Які різальні інструменти застосовують при виготовленні зубчастих коліс?

14. Яку пряму на рейці називають ділильною?

15.

Дата добавления: 2015-10-13