Передаточні механізми з рухомими осями

Передаточні механізми з рухомими осями сателітів поділяються на механізми з одним ступенем свободи () і на механізми, в яких . Механізми одним ступенем свободи можуть бути планетарними (рис. 2.3, в) або замкненими диференціальними (рис. 2.3, г), інші –– диференціальними (рис. 2.3, б).

а	б	в	г

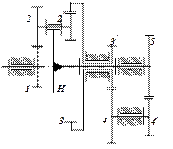
Рис. 2.3. Передаточні механізми: а – двохступінчаста співвісна передача; б - диференціальний механізм; в – планетарний механізм з мішаним зачепленням сателітів; г – замкнений диференціальний механізм

Планетарні зубчасті передачі дозволяють передавати більші потужності і реалізувати більші передаточні числа при меншому числі зубчастих коліс, чим передачі з нерухомими осями, через що вони набули великого поширення в сучасних машинах. За допомогою диференціальних механізмів можна передавати рух одному валу від двох або більше інших валів, які обертаються незалежно один від одного. Існує кілька методів визначення кінематичних характеристик планетарних і диференціальних механізмів, з яких розглянемо аналітичний метод, що ґрунтується на принципі оберненого руху.

В зубчастому механізмі з двома ступенями свободи (рис. 2.3, б) неможливо поставити й розв’язати задачу про визначення передаточного відношення. Можливо лише встановити зв’язок між трьома кутовими швидкостями w₁, w₃ і w _H, дві з яких незалежні. Кінематичний розрахунок механізмів з рухомими осями можна виконати із застосуванням методу інверсії або зверненого руху. У загальному випадку співвідношення між швидкостями коліс визначаються за формулою Віліса

, (2.4)

де – передаточне відношення оберненого механізму, який виникає з наданого механізму при зупинці водила , 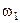– кутова швидкість ведучого валу; 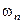– кутова швидкість вихідного валу механізму.

Таким чином для дослідження диференціального механізму з двома ступенями свободи необхідно знати дві кутових швидкості. Третю швидкість для наданої кінематичної схеми можна визначити за формулою (2.4) після розрахунку передаточного відношення оберненого механізму за відомими числами зубів коліс.

2.5.1. Передаточні відношення планетарних механізмів

В більшості планетарних механізмів кінематична схема виникає з відповідної схеми диференціального механізму при зупинці центрального колеса. Таке нерухоме колесо називається опорним колесом. Для опорного колеса за номером кутова швидкість . При підстановці в формулу (2.4) одержимо . Якщо ведучою ланкою є сонячне колесо 1, тоді відношення швидкостей буде передаточним відношенням планетарної передачі, . Таким чином, виходячи з формули Віліса, маємо

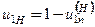. (2.5)

Послідовність розрахунків передаточних відношень розглянемо на конкретному прикладі.

Дата добавления: 2015-10-13