Анализ и принятие решений в условиях неопределенности и риска

Для эффективного анализа и принятия управленческих решений необходимо прежде всего определиться с областями риска. Областью риска называется некоторая зона общих потерь, в границах которой потери не превышают предельного значения установленного уровня риска.

В ходе анализа выделяется зона допустимого, критического и катастрофического риска. В зоне допустимого риска – потери не превышают ожидаемой прибыли, и предпринимателю угрожает недополучение прибыли. В пределах зоны допустимого риска данный вид предпринимательской деятельности сохраняет свою целесообразность. Граница зоны – уровень потерь, равный расчетной прибыли.

Зона критического риска характеризуется опасностью потерь свыше величины ожидаемой прибыли и вплоть до величины полной выручки от реализации, т.к. приводит к не возмещению и утере всех средств, вложенных в дело.

Зона катастрофического риска – это область потерь, которые достигают величины, равной имущественному состоянию предпринимателя.

Критериями риска, могут быть либо вероятность определенного уровня потерь (степень риска), либо то, что потери (риск) будут выше него.

Величина потерь Пв – наиболее вероятный уровень потерь. Вероятность их возникновения Рв – наиболее вероятный уровень риска. Величина Пв может быть вычислена в абсолютном выражении, в доле потерь от расчетной суммы выручки. Рдп – вероятность предельно допустимого риска, потери (Пдп) равны сумме ожидаемой прибыли. Ркр – вероятность критических потерь, а величина этих потерь (Пкр) равной полной расчетной сумме выручки. Ркт – вероятность катастрофического риска, величина катастрофических потерь (Пкт) равна всему состоянию предприятия.

При построении кривой необходимо исходить из следующих предположений:

Вероятность отсутствия потерь равна 0.

Вероятность исключительно больших потерь также равна 0, т.к. реальные потери имеют предел.

Существует конечная (меньшая 1) максимальная вероятность определенного уровня потерь, т.к. естественно предположить, что какой-то уровень потерь – наиболее вероятен.

Функция P=f (П) является непрерывной, монотонно возрастающей от 0 до max и убывающей в обратном порядке по мере увеличения уровня возможных потерь.

Предприниматель, оценивающий риск, интересуется, на сколько вероятно потерять сумму, находящуюся в определенном интервале. Наличие кривой вероятности потерь позволяет ответить на этот вопрос путем нахождения среднего значения вероятности в заданном интервале потерь.

Еще важнее знать вероятность того, что потери не превзойдут некоторого уровня. При построении кривой на рисунке 15 сделаны предположения:

- вероятность потерь больших 0, равна 1.

- с возрастанием уровня потерь вероятность превышения этого уровня монотонно убывает.

При неограниченном возрастании уровня потерь вероятность его превышения стремится к 0.

Эти допущения (как и к предыдущей кривой) условны и кое в чем спорны.

Показателями риска могут служить:

-показатель допустимого риска (Рдп) – вероятность того, что потери окажутся выше предельно допустимого уровня (Пдп);

-показатель критического риска (Ркр) – вероятность того, что потери окажутся выше предельного критического уровня (Пкр);

-показатель катастрофического риска (Ркт) – вероятность того, что потери превысят предельный катастрофический уровень (Пкт).

Необходимо установить предельные величины этих рисков, чтобы не попасть в зону неприемлемого риска. Такие величины называются критериями допустимого, критического и катастрофического риска – Кдп, Ккр, Ккт.

Общие условия приемлемости данного вида предпринимательства таковы:

Рдп ≤ Кдп; Ркр ≤ Ккр; Ркт ≤ Ккт.

Вся сложность состоит в расчете этих величин, для которых существуют только самые общие рекомендации.

При проведении анализа вероятных потерь необходимо предусмотреть все виды ущерба, чтобы учесть все источники риска. Если есть доминирующий вид ущерба, либо по вероятности, либо по величине, то можно рассматривать только его.

При анализе потерь необходимо отделить случайные составляющие от систематических. При потерях, приводящих к риску, необходимо учитывать только случайные потери, а все предвидимые потери должны быть включены в калькуляцию.

Если потери двух видов независимы и случайны, то вероятность общих потерь определяется по формуле:

где В0 – вероятность общих потерь, В1, В2 – вероятность потерь 1-го и 2-го вида соответственно рисунку 16.

В других литературных источниках предложены основные области риска, которые, по мнению авторов должны приниматься при расчете общего уровня риска с учетом достаточности капитала. При оценке достаточности капитала учитываются уставный капитал и весь капитал, т.е. достаточность капитала определяется максимально допустимым размером ее уставного капитала и предельным соотношением всего капитала компании к сумме ее активов, называемым коэффициентом риска (Н).

Безрисковая область (О – Г) характеризуется отсутствием каких-либо потерь при совершении операций с гарантией получения, как минимум расчетной прибыли. Теоретически прибыль фирмы при выполнении проекта не ограничена. Коэффициент риска Н1 = 0, где индекс 1 – первая область.

В 0,8 0,6 0,4 0,2    

Область минимального риска (О – А1 ≤ О – А) с уровнем потерь, не превышающем размеры чистой прибыли в интервале О – А. Коэффициент риска Н2 = НО – А1 во второй области находится в пределах 0 – 25%. С минимальным риском возможны операции с государственными ценными бумагами, получение необходимых ссуд, гарантированных правительством, участие по выполнению работ по строительству, финансированных государственными органами. Фирма рискует тем, что в результате своей деятельности в худшем случае она не получит своей прибыли, т.к. будут покрыты все налоги и она не сможет выплатить дивиденды по выпущенным ценным бумагам. Возможны случаи незначительной потери, но основная часть чистой прибыли будет получена. Области риска представлены на рисунке 14.

Потери Выигрыш

V

IV

III

II

I

Г1 В1 Б1 А1 О А Б В Г

Область недопустимого риска

Область критического риска

Область повышенного риска

Область минимального риска

Безрисковая область

Рисунок 14 - Основные области риска

Область повышенного риска (А – Б1 ≤ О – Б) характеризуется уровнем потерь, не превышающим размеры расчетной прибыли. Коэффициент риска Н3 = НА1-Б1 в третьей области находится в пределах 25-50%. В этой области возможно осуществление фирмой производственной деятельности, в том числе за счет получения кредитов в инвестиционных компаниях и банках на срок до одного года, за минусом ссуд, гарантированных правительством. Фирма рискует тем, что в результате своей работы она в худшем случае произведет покрытие всех затрат, а в лучшем – получит прибыль намного меньше расчетного уровня.

Область критического риска (Б – В ≤ О – В) – область с уровнем потерь, величина которых превышает размеры расчетной прибыли, но не превосходит общей величины валовой прибыли. Коэффициент риска II = II в четвертой области находится в пределах 50 – 75%. В этой области фирма может осуществлять различные виды лизинга: оперативный лизинг (аренда продукции вместо реализации), лизинг недвижимости (передача в аренду целевых объектов сроком на 15 – 20 лет); финансирующий лизинг (лизинговые компании передают в аренду машины и оборудование сроком от 2 до 6 лет); приобретение ценных бумаг других акционерных обществ и предприятий. Такой риск не желателен, т.к. фирма подвергается опасности потерять всю свою выручку от данной операции.

Область недопустимого риска (В1 – Г1 ≤ О – Г) – это область возможных потерь, близких к размеру собственных средств, т.е. наступление полного банкротства фирмы. В этом случае просроченная задолженность по ссудам составляет 100%, большой риск связан с вложением денежных средств и имущества в залог под банковские кредиты. Коэффициент риска Н5 = НВ1 – Г1 в пятой области находится в пределах 75 – 100%. Область недопустимого риска соответствует зоне катастрофического риска, а область повышенного риска – зоне допустимого риска.

Интересную классификацию поведения лиц, идущих на хозяйственный риск предложили венгерские авторы. Они отмечают, что если имеющиеся данные позволяют определить, какие по величине коэффициенты риска сопутствуют реальной экономической деятельности, то на основании математических или экономических соображений с помощью коэффициентов риска можно таким образам охарактеризовать поведение лиц, идущих на риск так: пессимистическое, осторожное, со средней степенью риска, азартное. Эта градация зависит от того, сколько категорий поведения в области принятия риска можно установить. На рисунке 15 представлена ориентировочная шкала риска.

Одинаково плохо, если таких категорий слишком мало или если их слишком много. По мнению венгерских ученых, наиболее целесообразно использовать 5 – 6 групп.

Классифицировать риск можно по масштабу хозяйственной деятельности, т.е. на основании какого статистического множества определяются границы категорий: все народное хозяйство, сектор, отрасль и т.д. Значение коэффициента риска может означать риск разного масштаба по отношению к химической промышленности и по отношению, например, к деревообрабатывающей промышленности.

Более тонкий анализ требует наличия различных шкал риска для каждого хозяйственного пространства.

Поскольку все проблемы, связанные с принятием решений, имеют вполне определенную структуру, состоящую из нескольких основных элементов, можно разработать общую модель принятие решений.

Как уже указывалось, существуют различия между понятиями риск и неопределенность. О риске говорят в ситуации, когда существует несколько возможных исходов и имеется релевантный прошлый опыт, позволяющий возможные исходы обработать статистически. Неопределенность проявляется в том случае, когда есть несколько возможных исходов, но предыдущих статистических данных мало, и это не позволяет предсказать возможные исходы. Большинство решений в бизнесе можно отнести именно к категории неопределенности. Однако при проведении нашего анализа описанная выше разница между риском и неопределенностью большого значения не имеет, поэтому в определенном смысле можно пользоваться этими терминами как синонимами.

Модель принятия решений имеет следующие характеристики.

Цель или задача, которую хочет решить лицо, принимающее решение, например, максимизация прибыли или определение приведенной стоимости потоков денежных средств. Численное представление цели часто называется целевой функцией; она применяется для оценивания альтернативных вариантов действий и служить для выбора лучшего из этих вариантов.

Поиск альтернативных вариантов действий, позволяющих достичь поставленную цель.

Поскольку проблемы, связанные с решениями, проявляются в условиях неопределенности, необходимо рассмотреть те неконтролируемые факторы, которые могут проявиться при каждом возможном варианте действий и которые могут оказать влияние на результат при каждом возможном варианте действий. Эти неконтролируемые факторы называются событиями или внешними условиями. Например, в ситуации запуска на рынок нового продукта возможными внешними условиями могут быть случаи, когда такой же продукт выпускает конкурент, но по более низкой цене, или когда такого продукта никто больше не предлагает.

Набор конечных результатов (исходов) для различных возможных комбинаций действий и событий. Каждый результат зависит от выбранного варианта действий и конкретных внешних условий.

Возможные варианты действий Внешние условия (реакций конкурентов)	Возможны исходы	Вознаграждение
Запуск на рынок Х Никаких действий	Небольшое увеличение прибыли	?
Такой же продукт	Прибыль без изменений	?
Запуск на рынок У Лучший продукт	Небольшое снижение прибыли	?
Никаких действий	Большое изменение прибыли	?
Такой же продукт	Небольшое увеличение прибыли	?
Отказ запуска на рынок Х и У Лучший продукт	Большое снижение прибыли	?
Никаких действий	Прибыль без изменений	?
Предложение нового продукта	Большое снижение прибыли	?

-Точка принятие решений

--Возможные события

Рисунок 16 - Дерево решений

Измерение численного результата (вознаграждения) для каждого возможного исхода в единицах, отражающих степень достижения заданных целей. Чаще всего это выражается в денежном виде, например, прибыль или поток денежных средств, но в некоторых случаях предпочтительнее выражать в других показателях, например, времени, рыночной доле и т.п.

Возможность того, что какое-то событие или внешнее условие наступит, известно под термином вероятность. Как правило, она выражается в виде десятичной дроби, и при этом ее значение находится между 0 и 1, или в процентах. Значение 0 указывает на нулевую возможность тог, что анализируемое событие обязательно случиться. Вероятность, скажем, 0,4 означает, событие, как ожидается, произойдет четыре раза из десяти. Общая сумма вероятностей событий, которые могут произойти, должна составлять 1,0. Например, если педагог говорит, что вероятность того, что студент сдаст экзамен, равно 0,7, то это означает, что у студента шанс на сдачу экзамена равен 70%. Учитывая, что среди других возможных событий, связанных со сдачей экзамена, можно указать только провал на экзамене, то вероятность такого исхода будет равна 0,3.

Информация может быть представлена в виде распределения вероятностей. Это список возможных исходов для анализируемого события и вероятности того, что исход наступить. Распределение вероятности для описанного выше примера имеет следующий вид:

Исход	Вероятность
Сдача экзамена	0,7
Провал экзамена	0,3
Итого	1,0

Некоторые вероятности также известны как объективные вероятности, поскольку могут быть вычислены математические или получены на основании исторический достоверных данных. Примерами объективных вероятностей могут быть: подбрасывание монеты или выбрасывание игровой кости. Например, вероятность того, что монета при ее подбрасывании ляжет «орлом» вверх, логически должна составлять 0,5. Это можно проверить на опыте, подбрасывая монету много раз и фиксируя полученные результаты. Аналогично, вероятность поучения цифры 1 при выбрасывании кости равна 0,166(т.е. одна шестая). Это тоже можно объяснить логически и проверить, многократно бросая игральную кость и фиксируя получаемые результаты.

Однако для решений в сфере бизнеса получение объективных вероятностей маловероятно, поскольку в этом случае часто предыдущих данных или повторно проводящихся процессов не бывает. Вероятности здесь приходится оценивать менеджерам на основе собственных суждений. Вероятности, полученные таким способом, называются субъективными вероятностями, поскольку скорее всего в таких условиях даже два человека редко присвоят конкретному исходу одни и те же значения вероятности. Субъективные вероятности оцениваются на индивидуальных знаниях, прошлом опыте и наблюдениях за текущими переменными, которые, возможно, влияют на результат будущих событий. Поэтому маловероятно, что такие вероятности могут быть оценены точно, т.е. любые оценки будущих неопределенных событий связаны с субъективными ошибками.

Преимущество этого подхода в том, что он обеспечивает более обоснованную информацию, которая позволяет указать наиболее вероятный исход. Рассмотрим, например, ситуацию, в которой преподавателя спрашивают о том, сдадут ли экзамен студенты А и В. Преподаватель может ответить, что оба студента, как он ожидает, экзамен сдадут. Это оценка преподавателя с точки зрения наиболее вероятного исхода. Однако более предпочтительно использовать в этом случае распределение вероятностей.

Таблица 3 - Распределение вероятностей

Исход	Вероятность для студента А	Вероятность для студента В
Сдача экзамена	0,9	0,6
Провал экзамена	0,1	0,4
Итого	1,0	1,0

Такое распределение вероятностей требует от преподавателя уточнить степень его уверенности в том, каковы будут возможные результаты будущего события. Понятно, что такая информация более значимо, чем простая оценка того, что оба студента, вероятно, сдадут предстоящий экзамен, поскольку показывает, что вероятность того, что студент А экзамен провалит, мала, в то время как для студента В это вполне возможно. Теперь применим принципы теории вероятностей к принятию решений в бизнесе.

Для менеджеров представление распределения вероятностей для каждого альтернативного варианта действий может дать полезную дополнительную информацию, поскольку такое распределение показывает степень неопределенности, которая существует для каждого из этих вариантов. Распределение вероятностей позволяет менеджерам рассматривать не только возможные прибыли (вознаграждения) для каждого альтернативного варианта, но и степень неопределенности этого варианта. Рассмотрим ситуацию, представленную в следующем примере

Таблица 4 - Распределение вероятностей для продукта А

Исход по прибыли	Оцениваемая вероятность	Взвешенное значение
	0,1
	0,2
	0,4
	0,2
	0,1
	1,0	8000(ожидаемое значение)

Таблица 5 - Распределение вероятностей для продукта В

Исход по прибыли	Оцениваемая вероятность	Взвешенное значение
	0,05
	0,1
	0,4
	0,25
	0,2
	1,0	8900(ожидаемое значение)

Менеджер рассматривает целесообразность выпуска продукта А или В, причем одновременно может производиться только один из них. Оцениваемый спрос по каждому продукту неизвестен. Подробное исследование возможного спроса по каждому продукту дает следующее распределение вероятностей прибыли по каждому из них.

Какой продукт компаний выгоднее выпускать?

Из распределения вероятностей, показанных в примере, видно, что существует один шанс из десяти, что прибыль для продукта А составит 6000 д. ед. и четыре шанса из десяти, что она будет д. ед. 8000. Более полезный способ анализа распределения вероятностей связан с тем, что компания по продукту А получит прибыль д. ед.8000 или меньше в семи случаях из 10. Это цифра получается сложением вероятностей для прибыли в д. ед. 6000, д. ед. 7000,и д.ед. 8000. Аналогично можно показать, что у компании вероятность получения прибыли в д. ед. 9000 и больше будет три из десяти.

Ожидаемые значение (иногда его называют ожидаемым вознаграждением) вычисляется взвешиванием каждого уровня прибыли (возможного исхода) в примере 12.2 на соответствующую ему вероятность. Сумма этих взвешенных величин называется ожидаемым значением для распределения вероятностей. Другими словами, ожидаемое значение это взвешенное среднее арифметическое возможных исходов. Для продуктов А и В ожидаемые значение в д. ед.8000 и в д. ед.8900 определяются с учетом не единственного варианта развития событий (единственное наиболее вероятной оценки), а диапазона возможных исходов. Например, единственная наиболее вероятная оценка-это уровень прибыли, который компания получит с наибольшей вероятностью. Для обоих продуктов в рассматриваемом примере наиболее вероятной оценкой является прибыль в д. ед.8000, а от продукта В д. ед.8900. Ожидаемые значение - это средние результаты возможных исходов, получаемые на основе менеджерских оценок.

Но нет никаких гарантий, что фактические исходы будут равны ожидаемым. Действительно, ожидаемое значение для продукта В распределении вероятностей как таковое не показано.

Помимо ожидаемых значений прибыли для различных альтернативных вариантов менеджеров также интересует степень неопределенности ожидаемых будущих прибылей. Например, предположим, что появилось возможность для еще одного варианта действий, т.е. если вернуться к примеру, то теперь можно выпускать и продукт С. В этом случае распределение вероятностей будет следующим.

Таблица 6 - Распределение вероятностей для продукта C

Исход	Ожидаемая вероятность	Взвешенное значение
Убытки 4000	0,5	-2000
Прибыль 22000	0,5
		9000 (ожидаемое значение)

Продукт С имеет более высокое ожидаемое значение, чем продукты А и В, но маловероятно, что менеджеры предпочтут продукт С продукту В; слишком высока у него изменчивость возможных исходов. Другими словами, у продукта С более высокая степень неопределенности.

Удобным показателем отклонения распределения вероятностей является стандартное отклонение. Это (s)- квадратный корень из среднеквадратического ожидаемого значения, вычисляется по формуле:

s= ,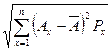

где 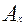-результат при конкретном уровне прибыли;

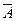- ожидаемое или среднее значение;

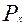-вероятность каждого исхода;

n-общее число возможных вариантов;

суммирование осуществляется по всем возможным вариантом.

Квадрат среднеквадратического отклонения (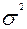) известен как статистическая дисперсия распределения и не должен смешиваться с отклонением от сметных или нормативных издержек. Вычисления среднеквадратических отклонений для продуктов А и В из примера показаны в таблицах 7, 8.

Таблица 7 - Вычисление среднеквадратических отклонений.

Продукт А

Прибыль	Отклонение от ожидаемого значения	Квадрат среднеквадратического отклонения	Вероятность	Взвешенное значение
	-2000		0,1
	-1000		0,2
		-	0,4	-
			0,2
			0,1
Сумма квадратов среднеквадратических отклонений
Среднеквадратическое отклонение	1095,40
Ожидаемое значение

Сравнивать среднеквадратические отклонения двух распределений вероятностей с различными ожидаемыми значениями напрямую нельзя. Почему? Чтобы разобраться в этом, рассмотрим распределение вероятностей для другого продукта, например D. Среднеквадратическое отклонение для продукта D равно 21424 д. ед., хотя во всех возможных исходах результат в 10 раз больше соответствующих исходов для продукта В.

Исходы для продукта D имеют такой же тип распределения вероятностей, как и для продукта В, и можно бы предположить, что риск, связанный с этими двумя продуктами, будет одинаковым. Но среднеквадратическое отколонение у продукта Д в 10 раз больше, чем у продукта В. Этот эффект масштаба может быть устранен при помощи замены среднеквадратического отклонения относительным показателем дисперсии. Относительный показатель дисперсии может быть выражен коэфициентом вариации, который представляет собой сренеквадратическое отклонение, деленное на ожидаемое значение. Коэффициент вариации для продукта В равен 2142,40 / 8900=0,241 (или 24,1%), а для продукта D- также 0,241 (21 424/89000), что указывает на то, что для обойх продуктов относительное значение дисперсии является одинаковым.

Таблица 8 - Вычисление среднеквадратических отклонений.

Продукт В

Прибыль	Отклонение от ожидаемого значения	Квадрат среднеквадратическое отклонение	Вероятность	Взвешенное значение
	-4900	24 010 000	0,05	1 200 000
	-2900	8 410 000	0,10	841 000
	-900	810 000	0,40	324 000
		1 210 000	0,25	302 500
		9 610 000	0,20	1 922 000
Сумма квадратов среднеквадратических отклонения Среднеквадратическое отклонение Ожидаемое значение	4 590 000
2142,40

Таблица 9 - Распределение вероятностей для продукта D

Исход по прибыли	Оцениваемая вероятность	Взвешенное значение
	0,05
	0,1
	0,4
	0,25
	0,2
	1,0	89000(ожидаемое значение)

В ходе проведенных рассуждений до сих пор риск определялся в единицах разброса возможных исходов, т.е. риск может быть большим даже в том случае, если все возможные исходы связаны с получением высокой прибыли. Однако риск, присущий возможным прибылям или убыткам, полученный при другом варианте действий, является не дисперсией как таковой, а прежде всего вероятностью того, что отклонения будут ниже ожидаемого значения. В данном случае лицо, принимающее решение, вряд ли станет рассматривать большие возможные отклонения, превышающие ожидаемое значение, как нежелательные (поскольку тогда просто прибыль будет больше). Рассмотрим следующие распределения вероятностей.

Среднеквадратические отклонения составляют д. ед.1342 для продукта Х и д. ед.2227-для У, что дает значения коэффициентов вариаций соответственно 0,19 (Х) и 0,28 (У). Эти показатели свидетельствуют о том, что оценкии для продукта У подвержены большей изменчивости, однако скорее всего продукт Х относится к категории с более высоким риском, так как вероятность того, что прибыль будет ниже д. ед.7000 (ожидаемое значенние Х), равна 0,4 для х и 0,2-для У. Понятно, что среднеквадратическое отклонение и коэффициент вариации не являются совершенными показателями риска, однако математические трудности измерения того, что эти отклонения ниже по величине ожидаемого значения,обычно очень значительны, если не говорит о самых простых случаях. Можно сказать, что ожидаемое значения, среднеквадратические отклонения и коэффициенты вариации используются для выражения обобщенных характеристик альтернативных вариантов действий, но сами по себе являются плохими заменителями для представления распределений вероятностей, так как не дают лицу, принимающему решение, всей релевантной информации. Поэтому появляется аргумент, чтобы предоставлять лицу, принимающему решение, непосредственно все распределение вероятностей. Такой подход вполне пригоден, когда менеджеры могут выбирать из небольшого числа альтернативных вариантов, но в ситуациях, когда вариантов возможных действий, которые необходимо рассмотреть, очень много; анализ многих распределений вероятностей скорее всего будет трудным и потребует много времени. В этих условиях у менеджеров может не оказаться большого выбора с точки зрения применяемых методов, и им ничего не останется, кроме сравнения ожидаемых значений и коэффициентов вариации.

Таблица 10 - Распределение вероятностей для продукта Х

Исход по прибыли	Оцениваемая вероятность	Взвешенное значение
	0,1
	0,3
	0,6
	1,0	7000(ожидаемое значение)

Таблица 11 - Распределение вероятностей для продукта У

Исход по прибыли	Оцениваемая вероятность	Взвешенное значение
	0,2
	0,5
	0,3
	1,0	8800(ожидаемое значение)

Как определить, является выбранный вариант действий рикованным или нет? Ответ на этот вопрос зависит от отношения к риску лица, принимающего решение. Можно выделить три возможных отношения к риску: отрицательное, положительное и нейтральное. Рассмотрим два варианта - А и В, которые характеризуются следующими возможными исходами в зависимости от состояния экономики (т.е. внешними условиями).

Таблица 12 - Возможные поступления

Состояние экономики	А, д. ед.	В, д. ед.
Спад
Нормальные условия
Бум

Если предложить, что три возмоожных состояния экономики равновероятны, то ожидаемое значение для каждого варианта составляет.100 д. ед. Лицо,положительно относящееся к риску,-это тот человек, который при выборе между вариантами сразличными степенями риска при одинаковых ожидаемых значениях, предпочитает более рискованный вариант (В). В тех же условиях лицо, отрицательно относящееся к риску, выбирает наименее рискованный вариант вариант (А). Лицо, безразличное к риску (нейтральное), может выбрать любой из двух вариантов, поскольку у них одно и тоже ожидаемое значение. Если говорить об инвесторах в целом, то исследования рынков ценных бумаг убедительно свидетельствуют, что большинство из инвесторов относятся к категории лиц, положительно относящихся к риску.

Рассмотрим, насколько полезны вычисления ожидаемых значений для выбора между альтернативными вариантами действий. Как выше сказано, ожидаемое значения представляют собой долгосрочные средние показатели, но решения не должны приниматься только на их значениях, поскольку это не позволяет учитывать отношение к риску лица, принимающего решение. Рассмотрим, например, ситуацию, когда два человека подбрасывают монетки и проигравший отдает победителю 5000 д. ед. Ожидаемое значение для игрока, который ставит на «орла», следующее:

Исход	Денежные поступление, д. ед.	Вероятность	Взвешенное значение, д. ед.
Орел	+5000	0,5	+2,500
Решка	-5000	0,5	-2,500
Ожидаемое значение

Ожидаемое значение в этом примере равняется нулю, но если игра состоится, то фактический ее исход будет не нулевым. Вычисление ожидаемого значения представляет средний исход только в том случае, если игра повториться в течение многих раз. Но если игра будет сыграна только раз, то маловероятно, что какой то игрок сочтет, что вычисленное ожидаемое значение с точки зрения принимаемого решения окажется для него полезной информацией. Фактически вычисленное ожидаемое значение исходит в данном случае из того, что каждый игрок безразлично относиться к результатам игры, а это может быть только в том случае, если оба игрока к риску нейтральны. А игрок, отрицательно относящийся к риску, посчитает, что это игра для него непривлекательна.

Поскольку большинство менеджеров в бизнесе, скорее всего, не могут быть отнесены к категории людей, которые относятся к риску нейтрально, и поскольку решения в бизнесе редко повторяются, необходимо дополнить их измерениями дисперсии, и там, где возможно, решения должны приниматься после сравнения распределения вероятностей при различных альтернативных вариантах действий.

В примерах, приведенных выше, принималось допущение, что размер прибылей является неопределенным из-за неопределенности спроса. На практике неопределенными могут быть более чем одна переменная (например, реализация и затраты), и при этом значения нескольких переменных могут зависеть от значений других переменных. В результате этого могут быть самые различные исходы, причем результаты одних исходов могут зависеть от предыдущих исходов. Полезным аналитическим инструментом для установления диапазона возможных вариантов действий и их возможных численных результатов является дерево решений.

Дерево решений - это диаграмма, показывающая несколько возможных вариантов действий и возможных событий, а также потенциальные исходы для каждого варианта действий. Здесь каждый вариант действий или события представлен отдельной ветвью, которая ведет к последующим ветвям, отражающим дальнейшие действия или возможные события. Дерево решений строится так, чтобы показать полный диапазон альтернатив и событий, которые могут произойти при всех анализируемых условиях. Ценность дерева решений определяется возможностью провести с его помощью логический анализ, позволяющий выбрать полную стратегию, учитывающую все возможные варианты до того, как компания выберет один из них. Рассмотрим следующий пример и воспользуемся им, чтобы показать, как дерево решений может применяться для принятия решений в условиях неопределенности.

Пример. Компания рассматривает, целесообразно ли ей разрабатывать новый продукт и выходить с ним на рынок. Затраты на разработку оцениваются в размере 180000 д.ед., и существует вероятность 0,75, что разработки будут успешными и 0,25 - что окончатся неудачей. Если разработки будут успешными, продукт будут выведен на рынок и при этом существуют следующие оценки:

1) если продукт будет очень успешным, прибыль составит д. ед.540 000;

2) если продукт будет средне успешным, прибыль составит д. ед.100 000;

3) если продукт «провалится», убытки составят д. ед.400 000.

Каждое из приведенных выше вычислений прибыли и убытков сделано с учетом затрат на разработку в размере д. ед.180 000. Оцениваемая вероятности для каждого из указанных выше событий следующие:

1 Высокая успешность	0,4
2 Средняя успешность	0,3
3 Провал	0,3

Дерево решений для этого примера должно быть построено на основании предыдущей модели и последующей методики.

Квадраты указывают точки, в которых решения должны приниматься, а ветви, исходящие из них, указывают на возможные варианты действий. Кружочки - это точки, в которых происходят изменения в условиях, влияющие на последствия от предыдущих решений. Ветви, выходящие из этих точек, указывают на возможные типы состояние окружающей среды (внешние условия).

Совместная вероятность двух событий, происходящих вместе -это вероятность одного события, умноженная на вероятность другого события. Например, вероятность того, что разработка окончится успехом и что продукт будет принят на рынке очень успешно, равна 0,75*0,4, что дает вероятность 0,3. Аналогично вероятность того, что разработка окончится успехом и что продукт будет принят на рынке достаточно (средне) успешно, равна 0,75*0,3, что дает вероятность 0,225. Общее ожидаемое значение в отношении решения о разработке продукта равно сумме всех элементов, входящих в графу для ожидаемых значений по ветви «Разработка продукта» дерева решений и составляет 49500 д.ед.. Если мы примем допущение, что других альтернативных вариантов, кроме решения не заниматься указанной разработкой, нет, то ожидаемое значение в 49500 д.ед для разработки продукта можно сравнить с ожидаемым значением в 0 д.ед. для варианта не занимается разработкой. Если следовать теории решений, то заняться разработкой продукта целесообразно, так как в этом случае ожидаемое значение является величиной положительной. Однако это совсем не означает, что прибыль в.49500 д.ед является гарантированной. Вычисления ожидаемого значения только показывают, что если вероятности событий заданы правильно и что если это решение будет повторено много раз, то средний размер прибыли составит 49500 д. ед.

К сожалению, решения в данном случае не будет повторяться много раз, и несколько последовательно понесенных убытков могут заставить компанию выйти из бизнеса до того, как у нее появится возможность повторить прежнее решение. Поэтому менеджеры при принятии решения о разработке продукта могут предпочесть изучение следующего распределения вероятностей:

Исход	Вероятность
Убытки в д. ед.400000	0,225
Убытки в д. ед.180000	0,25
Прибыль в д. ед.100000	0,225
Прибыль в д. ед.540000	0,30

После изучения этой информации менеджеры могут решить, что данный проект слишком рискованный, поскольку вероятность убытков близка к 0,5.

Таким образом, дерево решений является удобным способом идентификации всех возможных альтернативных вариантов действий и их взаимозависимостей. Этот подход особенно полезен при установлении распределения вероятностей, когда возможно большое число комбинаций.

Управленческие решения в современных условиях принимаются в ситуациях, которые подвержены ряду характеристик неопределенности. На методы принятия решения в условиях риска накладывает отпечаток многообразие критериев и показателей посредствам, которых оценивается уровень риска. Поэтому для принятия решений могут использоваться и другие методики.

В самом общем виде постановка и решение задач, оптимизация решений принимаемых в условиях риска, может быть предоставлено следующим образом:

Во-первых, имеется m – решений (Р1, Р2, Р3…Рm), определяющий ассортимент продукции.

Во-вторых, условия обстановки точно не известны, однако о них можно сделать n предложений (О1, О2, О3…Оn) эта обстановка может быть определена платежеспособным спросом.

В-третьих, результаты (прибыль, выигрыш) аn соответствует каждой паре сочетаний решений и обстановки, которая может быть представлена в виде взаимосвязи эффективности:

Таблица 13 - Взаимосвязь эффективности

Варианты решений Р	Варианты условий О
О1	О2	О3 …
Р1	а12	а12	а13
Р2 …

Таблица заполняется до конца при любом наборе.

Выигрыши, обозначенные в таблице, являются показателями эффективности решений. Следует отметить, что выбор решений в условиях риска предполагает, что вероятность возможных вариантов обстановки известны. Вероятность определяется либо статистическими, либо экспертными методами. Наличие выигрышей, определяющих эффективность решений в разных условиях обстановки, позволяет одновременно определить потери в результате принятия неоптимальных решений. Порядок определения потерь и выбор решений базируется на уже известном показателе: критерий риска: R = Hn * P

Риск равен наличию проигрышей умноженному на вероятность. Предпочтение согласно такому критерию отдается такому решению, которое имеет наиболее взвешенный риск.

Например: предприятия готовиться к переходу на новые виды продукции при этом возможны 4 варианты решения, каждому из которых соответствует определенный вид выпуска или их сочетание. Результаты принятых решений существенно зависят от обстановки, которая в значительной мере неопределенна. Пусть варианты обстановки характеризует структура спроса на новую продукцию и она может быть в трех типах О1, О2, О3. Выигрыш, характеризующий относительную величину результата прибыли соответствующей каждой паре сочетания:

Продукция Р	Варианты условий О (обстановки)
О1	О2	О3
Р1	0,25	0,35	0,40
Р2 …	0,75	0,20	0,30
Р3	0,35	0,82	0,10
Р4	0,80	0,20	0,35

На основании предложенных данных необходимо найти такую стратегию решений, которая по сравнению с другими является наиболее выгодной. Для принятия таких решений принимается специальный показатель потерь. Потери рассчитываются как разность между ожидаемым результатом действий, при наличии точных данных обстановки и результатом, который может быть достигнут, если эти данные не определены. Например, если точно известно, что наступит обстановка О1, то следует принимать решение Р4, но поскольку точно неизвестно, какую обстановку ожидать, то желательной обстановкой является О2 решение Р3. Если же принять решение Р3 в надежде на обстановку О2, и наступила обстановка О1, то величина каких потерь составила = 0,80-0,35 = 0,45.

В общем случае потери соответствующие каждой паре сочетаний определяются разностью между максимальным выигрышем и выигрышем при конкретном решение. На базе данных предыдущей таблицы можно составить таблицу потерь при выпуске новых видов продукции:

Решения	Обстановка
О1	О2	О3 …
Р1	0,55	0,47
Р2 …	0,5	0,62	0,1
Р3	0,45		0,3
Р4		0,72	0,05

При одинаковых показателях эффективности выпуска новых видов продукции - величины потерь могут быть различными. В дополнение к представленным расчетам можно внести следующую информацию: пусть вероятность первого варианта обстановки О1 = 0,5, второго - О2=0,3 и О3=0,2, тогда показатель риска для каждого из решений составит R = åHn * P.

Отсюда следует:

1 набор= 0,275+0,141+0 = 0,416

2 набор= 0,05*0,5+0,62*0,3+0,1*0,2=0,025+0,186+0,02 = 0,231

3 набор= 0,45*0,5+0*0,3+0,3*0,2 = 0,225+0,06 = 0,285

4 набор= 0*0,5+0,72*0,3+0,05*0,2 = 0,186+0,01 = 0,226

При заданном условии Р4 менее рисковый.

Такой подход к принятию решений в условиях неопределенности дает вероятностные результаты анализа возможных вариантов.

При принятии решений в условиях неопределенности, когда вероятности возможных вариантов обстановки неизвестны, применение выше представленной методики невозможно. При принятии решений в таких ситуациях рекомендуется ориентироваться на критерии, применения которых соответствует характеру задач, целевым установкам, и склонности к риску лица принимающего решения. К числу классических критериев относят:

- принцип недостаточного обоснования Лапласа;

- максимальный критерий Вальда;

- минимальный критерий Сэвиджа;

- критерии обобщенного максимина Гервица.

Принцип недостаточности обоснования Лапласа, используется в случае если можно предположить, что любой из варианта обстановки не более вероятнее чем другой. Тогда вероятности обстановки можно считать равными и производить выбор решения, также как и в условиях риска, то есть по минимальному средневзвешенному показателю риска.

Максимальный критерий Вальда, используется в случаях, когда требуется гарантия того, чтобы выигрыш в любых условиях оказался не менее чем наибольший из них в худших условиях. Наибольшим решением будет тот, для которого выигрыш окажется максимальным из всех минимальных при различных вариантах условия. Этот критерий ориентируется на максимальный гарантированный выигрыш, который может быть получен.

Минимальный критерий Сэвиджа, используется в тех случаях, когда требуется в любых условиях избежать большого риска. В соответствии с этим критериям предпочтение следует отдать решению, для которого потери при различных вариантах условий окажутся минимальными.

Критерии Вальда и Сэвиджа относятся к разряду осторожных.

Критерий обобщенного максимина (оптимизма и пессимизма) Гурвица, используется, если требуется установить между линией поведения в расчете на худшее и линией поведения в расчете на лучшее.

Общую модель принятия решений в условиях неопределенности можно охарактеризовать следующими этапами:

1 установление (определение) целей. В качестве цели, которое хочет достичь лицо, принимающиеся решение может быть – максимизация прибыли, минимизация убытка, максимальная приведенная стоимость денежных потоков. Численное представление цели называют целевой функцией, которую используют для сравнения альтернативных вариантов и выбора наилучшего из них.

2 Поиск возможных направлений действий, позволяющих достичь постоянную цель.

3 Выявление возможных внешних условий, то есть выявление неконтролируемых факторов, которые могут появиться при каждом варианте действий и которые могут оказать влияние на результат при каждом из них.

4 Перечисление возможных конечных результатов, учитывая, что возможный исход зависит от выбранного варианта действий и конкретных внешних условий.

5 Измерение результата количественно для каждого возможного исхода;

6 Выбор оптимального варианта действий.

Таким образом, существующие методы оценки риска многообразны и в зависимости от конкретной ситуации применяются в экономических расчетах.

Дата добавления: 2015-10-13