Понятие функции полезности

Пусть имеется множество объектов, которые индивидуум может сравнивать по их предпочтительности для себя, т.е. он в состоянии указать, какой объект является для него предпочтительным. Если, опираясь на результаты проведенных сравнений, можно приписать сравниваемым объектам количественные оценки так, чтобы более предпочтительному объекту соответствовала большая оценка, то функция, которая устанавливает такое соответствие, называется функцией полезности. Функции полезности осуществляют возможность перехода от качественных сравнений объектов к их количественным оценкам, т.к. приписывают каждой альтернативе некоторое число - его полезность.

К основным теоремам теории полезности относят аксиомы предпочтения, которые обеспечивают способность ставить в соответствие каждой альтернативе некоторое число (полезность) таким образом, что для любых двух альтернатив одна предпочтительнее другой, если полезность первой превосходит полезность второй. В теории ожидаемой полезности рассматривают «сравнения по предпочтению альтернатив, последствия которых неопределенны, и условия, которые не только обеспечивают существование на множестве альтернатив функций полезности, сохраняющих упорядочение, но и дают возможность представить полезность альтернативы в виде математического ожидания, используя полезности последствий и их вероятности».

Теория оценивания риска посвящена правилам выбора или сравнения (предпочтения) ситуаций, связанных с риском. Общая теория риска рассматривает общие универсальные правила сравнения, не привязанные к конкретным экономическим ситуациям. «При этом апеллируют к некоторым естественным или кажущимся таковыми нормативным правилам (аксиомам), которые отражают те или иные аспекты «экономической интуиции».

Формально общая теория риска занимается предпочтениями или правилами сравнения случайных величин либо распределений вероятностей (в т.ч. будущего дохода). Принимается как очевидное правило первого стохастического доминирования, которое можно выразить так: «больше - лучше». При сравнении случайных величин это означает, что если при любом состоянии природы случайная величина Х не меньше случайной величины Y, то Х не хуже Y. При сравнении распределений вероятностей это правило формулируется так: если для функций распределения F(x) и G(х) верно, что F(х) 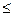G(х) для всех х, то F(х) не хуже G(х).

Если рассматривать только исчисляемые предпочтения, т.е. правила сравнения, при которых «качество» той или иной случайной величины будущего дохода можно охарактеризовать числом, то это означает существование такой функции (функционала) U(х), при котором случайная величина Х «лучше» случайной величины У тогда и только тогда, когда U(х) > U(y).

Функционал U(х) называют функционалом полезности.

Понятие функции полезности ввел Д. Бернулли, который называл ее «нравственным ожиданием». Предполагается, что «полезность», испытываемая индивидуумом от детерминированного дохода х, возрастет не пропорционально х, но ее можно измерить, в общем случае, нелинейной функцией u(х). Если предположить, что приращение полезности пропорционально не абсолютному, а относительному изменению дохода, т.е. du = k · dx/x, где k – некоторый коэфициент, то u(x) = k · 1n(x) + const. Д. Бернулли рассматривал именно эту функцию.

Полезность детерминированного дохода изменяется самим доходом:

u(x) = M(x), (1)

где M(x)- математическое ожидание х.

Если доход представлен случайной величиной Х, то случайна и величина полезности u(x), а ее среднее значение равно

U (x) =M · u(x), (2)

Если Х принимает конечное число значений х₁, …, х_N с вероятностями р₁, …, р_N, то критерий сравнения имеет вид

U(x)= 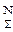u(x_i)·P_i, (3)

В общем случае для случайной величины Х с функцией распределения F(x) функция полезности равна

U(x)= u(x)dF(x), (4)

Этот критерий совпадает со средним значением в частном случае u(x)=x.

При выполнении правила первого стохастического доминирования u(X) не убывает. Выпуклость функции вниз (вверх) отражает склонность (не склонность) к риску. Так, неравенство Йенсена утверждает, что если u(X) функция выпуклая вверх, то M u(x) 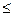u(MX).

Это неравенство означает, что индивидуум с выпуклой вверх функцией полезности случайному доходу предпочтет детерминированный доход, равный математическому ожиданию МХ.

С помощью модели, в которой функция полезности подбирается выпуклой вверх при низких и выпуклой вниз при высоких уровнях доходов, может быть объяснено поведение людей, охотно идущих на небольшой риск, например, покупая лотерейные билеты, но страхующих свое имущество, избегая риска, связанного с большими потерями.

В теории риска критерии сравнения выводятся из аксиом, которым должны удовлетворять отношения предпочтения. В теории ожидаемой полезности основной является аксиома независимости.

Пусть имеется три случайные величины y₁, y₂, z (тот или иной вариант получения случайного дохода). Для любого 0 < a < 1 обозначим y_a случайную величину, соответствующую ситуации, когда с вероятностью а выбирается вариант y₁ и с вероятностью 1 – а – вариант z. Пусть y'_a – величина составленная, составленная по тому же правилу из y₂ и z. Тогда аксиома независимости состоит в следующем: если y₁ «лучше» y₂, то y_а, лучше y'_a для любого а, т.е. «смешивание» y₁ и y₂ с одной и той же величиной (z) не меняет предпочтений. Эта аксиома, как показывает теория, в сочетании с некоторыми другими приводит к линейной модели.

По мнению многих специалистов, линейная теория полезности является недостаточно гибкой, не отражает всего многообразия возможных ситуаций. Появились нелинейные модели оценивания риска: модель ожидаемой полезности с ранжированными вероятностями, критерий взвешенной полезности, критерии, связанные с понятием сравнительной или неявной полезности, линейная комбинация математического ожидания и дисперсии и др. Но пользоваться ими следует осторожно, т.к. они либо не удовлетворяют правилу первого стохастического доминирования, либо могут быть применимы лишь в «спокойной» ситуации, когда можно оценивать каждый новый риск вне зависимости от всего портфеля взятых ранее рисковых обязательств, т.е. когда мала вероятность разорения.

Несмотря на бурное развитие нелинейной теории, линейная модель остается весьма распространенной во многих областях экономических исследований. Хотя она дает довольно грубое приближение к истинной мере риска, во многих случаях это приближение оказывается достаточным, особенно на фоне недостатка конкретной информации, статистических данных и т.п.

Кроме того, практически всегда линейный функционал можно рассматривать как линейную часть приращения нелинейных функционалов. Это дает возможность пользоваться локальной функцией полезности, свойства которой аналогичны свойствам «обычной» функции полезности.

Дата добавления: 2015-10-13