Пример 4

Все пространство является подпространством в

[11] Предложение 4. Пусть подпространство n-мерного пространства . Тогда 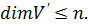Если то совпадает с

Действительно, любая система из векторов в лежит также и в и потому линейно зависима. Пусть базис в содержит векторов. Тогда любой вектор из раскладывается по этому базису и, следовательно, принадлежит . Значит, совпадает с .

Предложение 5. Пусть подпространство n-мерного пространства . Если базис ,..., в дополнить до базиса в , то в таком базисе все векторы из и только они будут иметь компоненты

Действительно, если для вектора 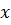имеем , то

и, следовательно, . Обратно, вектор из раскладывается в линейную комбинацию Она же есть разложение 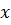по базису ,..., при

Заметим, что равенства можно рассматривать как систему линейных уравнений, связывающую координаты вектора 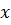. Нетрудно доказать, что и в любом другом базисе определяется системой линейных уравнений. Действительно, при замене базиса старые компоненты выражаются через новые, и в новом базисе система уравнений примет вид

, …, .

Ранг этой системы равен , поскольку строки матрицы перехода линейно независимы. Итак, мы доказали.

Предложение 6. Пусть в n-мерном пространстве выбран базис. Тогда координатные столбцы векторов, принадлежащих k-мерному подпространству удовлетворяют однородной системе линейных уравнений ранга

Дата добавления: 2015-10-13