Глава III . Сумма и пересечение подпространств

Рассмотрим два подпространства линейного пространства .

Определение. Будем называть суммой подпространств и обозначать линейную оболочку их объединения .[6]

Подробнее определение означает, что вектор из (и только такой) представим в виде 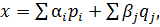где векторы лежат в а в Обозначая написанные выше суммы через и 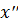, мы видим, что подпространство состоит из векторов, представимых в виде:

где а

Пусть размерности подпространств равны и . Выберем в этих подпространствах базисы 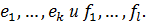Каждый вектор из раскладывается по векторам 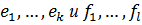, и мы получим базис в , если удалим из этой системы все векторы, которые линейно выражаются через остальные. Сделать это можно, например, так.

Выберем какой-либо базис в и составим матрицу из координатных столбцов всех векторов 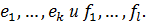Те векторы, координатные столбцы которых базисные столбцы этой матрицы, составляют базис в .

Определение. Назовем пересечением подпространств и обозначим множество векторов, которые принадлежат обоим подпространствам.

Пересечение есть подпространство. Действительно, нулевой вектор лежит во всех подпространствах и, следовательно, пересечение не пустое множество. Если векторы лежат в , то они лежат как в , так и в . Поэтому вектор и при любом ⍺ вектор также лежат и в , и в , а следовательно, и в .

В конечномерном пространстве подпространства могут быть заданы системами линейных уравнений. Тогда их пересечение задается системой уравнений, получаемой объединением систем, задающих подпространства.

Для подпространств сумма и пересечение определяются аналогично, и полученные выше свойства переносятся на суммы и пересечения подпространств.

В частности, суммой подпространств 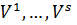называется линейная оболочка их объединения. Это множество всех векторов, представимых в виде суммы , где 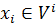Каждый из векторов может быть разложен по базису в своем подпространстве , и потому любой вектор из суммы 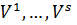раскладывается по системе векторов, получаемой объединением базисов всех подпространств. Число векторов в этой системе равно Поскольку векторы всех базисов в совокупности могут быть линейно зависимыми, размерность суммы подпространств может оказаться меньше общего числа векторов в системе:

Базис в сумме подпространств получается, как и при 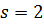, из объединения базисов слагаемых удалением векторов, линейно выражающихся через остальные.[7]

Определение. Сумма подпространств называется прямой суммой, если ее размерность равна сумме размерностей этих подпространств, т. е. имеет максимальное из возможных значений.

Если надо подчеркнуть в обозначении, что сумма прямая, то используют знак .

Прибавление нулевого подпространства не меняет ни размерность суммы, ни сумму размерностей. Но ниже мы будем считать подпространства ненулевыми, чтобы избежать оговорок, вызванных несуществованием базиса в нулевом подпространстве.

Предложение 1. Для того чтобы сумма подпространств была прямой суммой, необходимо и достаточно выполнение любого из следующих четырех свойств:

а) любая система из ненулевых векторов, принадлежащих

различным подпространствам линейно независима;

б) каждый вектор однозначно раскладывается в сумму , где

в) пересечение каждого из подпространств с суммой остальных

есть нулевое подпространство;

г) объединение базисов подпространств базис в .

Доказательство. Мы докажем, что из определения прямой суммы следует свойство а), и каждое из свойств б), в) и г) следует из предыдущего. Поскольку из свойства г) непосредственно следует определение прямой суммы, это будет означать равносильность каждого из свойств определению.

1. Докажем от противного, что из определения следует свойство а).

Допустим, что нашлась линейно зависимая система ненулевых векторов таких, что никакие два из них не лежат в одном и

том же подпространстве . Дополним каждый из этих векторов до

базиса в его подпространстве, а в тех подпространствах, из которых

в системе векторов нет, выберем базис произвольно.

Объединение этих базисов система из векторов. Каждый вектор из раскладывается по этой системе, но система эта линейно зависима (так как она содержит линейно зависимую подсистему). Поэтому базис в содержит меньше, чем векторов, и размерность суммы меньше суммы размерностей.

2. Докажем, что из свойства а) следует свойство б). Допустим, что б) не выполнено и некоторый вектор 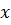представлен как сумма , и как сумма 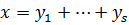, где . Тогда . Если хоть одна из разностей отлична от нуля, мы получаем противоречие со свойством а).[8]

3. Докажем теперь также от противного, что из свойства б) следует в). Не уменьшая общности, мы можем допустить, что имеет ненулевое пересечение с суммой . В этом случае существует ненулевой вектор , представимый в виде суммы 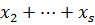. Но равенство

означает двумя способами представлен как сумма векторов, выбранных по одному из каждого .

4. Докажем, наконец, что из свойства в) следует г). Рассмотрим систему векторов, получаемую объединением базисов подпространств . Каждый вектор из суммы обязательно раскладывается по этой системе, и нам остается доказать, что при условии в) эта система линейно независима.

Сделаем это от противного. Допустим, что существует равная нулю нетривиальная линейная комбинация всех векторов, входящих в рассматриваемые базисы подпространств . Сгруппируем слагаемые в этой линейной комбинации так, чтобы объединить все слагаемые, относящиеся к одному подпространству. Мы получим равенство вида , где хотя бы один вектор отличен от нуля. Не уменьшая общности, можно считать, что это 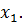Тогда , Это значит, что ненулевой вектор принадлежит также сумме . Получено противоречие со свойством в). Это заканчивает доказательство всего предложения.

Отметим как частный случай свойства в), что сумма двух подпространств прямая, если их пересечение нулевое.

Легко видеть, что при сложении подпространств можно произвольно расставлять и убирать скобки. Это относится и к прямой сумме. Например, ) ⊕( ⊕ .

Если , то . В частности, для любого подпространства .

Предложение 2. Для любого подпространства пространства найдется такое подпространство , что .

Доказательство. Выберем базис подпространства и дополним его до базиса пространства векторами . Линейную оболочку обозначим через . Из предложения 1 видно, что

.

Теорема 1. Размерность суммы двух подпространств равна сумме их размерностей минус размерность их пересечения.

Если сумма прямая, утверждение справедливо: размерность равна сумме размерностей, а пересечение нулевое.

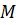Пусть теперь подпространства с ненулевым пересечением. Согласно предложению 2 найдется такое подпространство , что

Тогда Отсюда видно, что , так как

Докажем, что прямая сумма. Для этого рассмотрим произвольный вектор . Из следует , а следовательно, Отсюда , и пересечение нулевое. [9]

По определению прямой суммы . Кроме того, Вычитая эти равенства почленно, приходим к требуемому заключению.

Дата добавления: 2015-10-13