Пример 1.

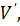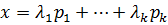Пусть дано некоторое множество векторов в линейном пространстве . Обозначим через совокупность всевозможных линейных комбинаций, каждая из которых составлена из конечного числа векторов из . Множество является подпространством в .[10] Действительно, если и принадлежат то и

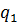
где , Мы видим, что

, т.к. также является линейной комбинацией конечного числа векторов из 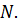Точно так же мы видим, что .

Так построенное подпространство называется линейной оболочкой множества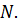

Пусть ,..., - линейно независимая система векторов из такая, что каждый вектор из по ней раскладывается. (Если пространство конечномерно, то очевидно, что в каждом множестве, содержащем ненулевые векторы, такая система найдется.) Векторы ,..., образуют базис в линейной оболочке . В самом деле, каждую линейную комбинацию векторов из можно представить как линейную комбинацию векторов ,..., , так как каждый вектор из можно разложить по ,..., и подставить эти разложения в рассматриваемую линейную комбинацию.

В частности, если - конечное множество векторов, мы имеем:

Предложение 3. Размерность линейной оболочки множества из векторов не превосходит .

Дата добавления: 2015-10-13