Определение линейного подпространства

В обычном геометрическом пространстве сумма векторов, лежащих в некоторой плоскости, также лежит в этой плоскости, и умножение вектора на число не выводит его из плоскости, в которой он лежит. Теми же свойствами обладают векторы, лежащие на прямой линии. Для линейных пространств обобщением плоскости и прямой служат линейные подпространства.[3]

Определение: непустое подмножество векторов линейного пространства V называется линейным подпространством, если:

а) сумма любых векторов из принадлежит ;

б) произведение каждого вектора из на любое число также принадлежит .

В силу этого определения любая линейная комбинация векторов из 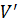принадлежит 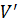. В частности, нулевой вектор как произведение 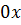должен принадлежать 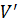, и для каждого 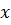из 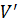противоположный вектор лежит в

Сложение и умножение на число, определенные в , будут такими же операциями в его подпространстве . Справедливость аксиом линейного пространства для прямо вытекает из их справедливости для . Таким образом, подпространство является линейным пространством.

Дата добавления: 2015-10-13