Линейное подпространство задано однородной системой линейных уравнений

Если линейное подпространство задано однородной системой линейных уравнений, то в задачах в данном случае чаще всего нужно найти размерность и ранг подпространства; или найти фундаментальный набор решений и обозначить базисные и свободные переменные. Отметим некоторые нюансы.[4]

1) Если

,

то базисные переменные, а 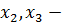свободные.

2) Ранг — это количество ненуливых различных строчек, оставшихся в матрице при её решении методом Жордана-Гаусса (метод заключается в том, чтобы в каждом столбце матрицы оставить лишь одну значащую цифру, а все остальные посредством домножения строчек на число и сложения/вычитания обратить в нули).

3) Ранг равен количеству базисных переменных.

4) Размерность — это количество векторов в базисе данного линейного подпространства, максимальное количество линейно-независимых векторов.

5) Размерность равна разности количества переменных и ранга. Это количество свободных переменных.

Дата добавления: 2015-10-13