Метод парабол.

Існують досить широкі класи функцій, які зручно апроксимувати, наприклад, многочленом другого степеня. Тоді за наближене значення мінімуму функції доцільно взяти точку мінімуму цього многочлена. Оскільки графік многочлена другого степеня має вигляд параболи, то такий метод називають методом парабол. Цей метод дає хороші результати при мінімізації гладких унімодальних функцій, тому що в околі точки графіки таких функцій досить "близькі" до параболи.

Для побудови апроксимуючого многочлена другого степеня необхідно мати три точки такі, що

,

i значення функції в цих точках .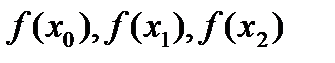

Тоді інтерполяційний многочлен Лагранжа другого степеня має вигляд:

,

або у більш зручній для диференціювання формі:

. (19)

Нехай унімодальна на функція i .

Означення 2. Трійка чисел називається вдалою, якщо

і

.

Остання умова означає, що точки , , 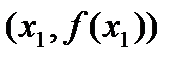не лежать на прямій, паралельній осі абсцис (рис. 10).

Із означення вдалої трійки випливає, що точка мінімуму функції міститься всередині відрізка .

Рис. 10.

Нехай знайдена вдала трійка чисел 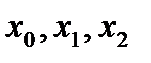. Тоді хоча б одна з нерівностей і строга i коефіцієнт при старшому члені многочлена (19) додатній.

Визначивши похідну многочлена (19) i прирівнявши її до нуля, можна показати, що мінімум досягається в точці

, (20)

при цьому .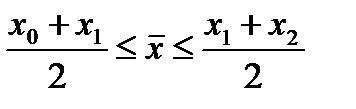

Отримана точка i обирається за точку наступного обчислення значення функції (рис. 11).

Можливий випадок, коли (рис. 12). Тоді за точку наступного обчислення обирається одна з точок

або .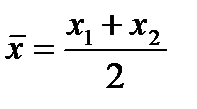

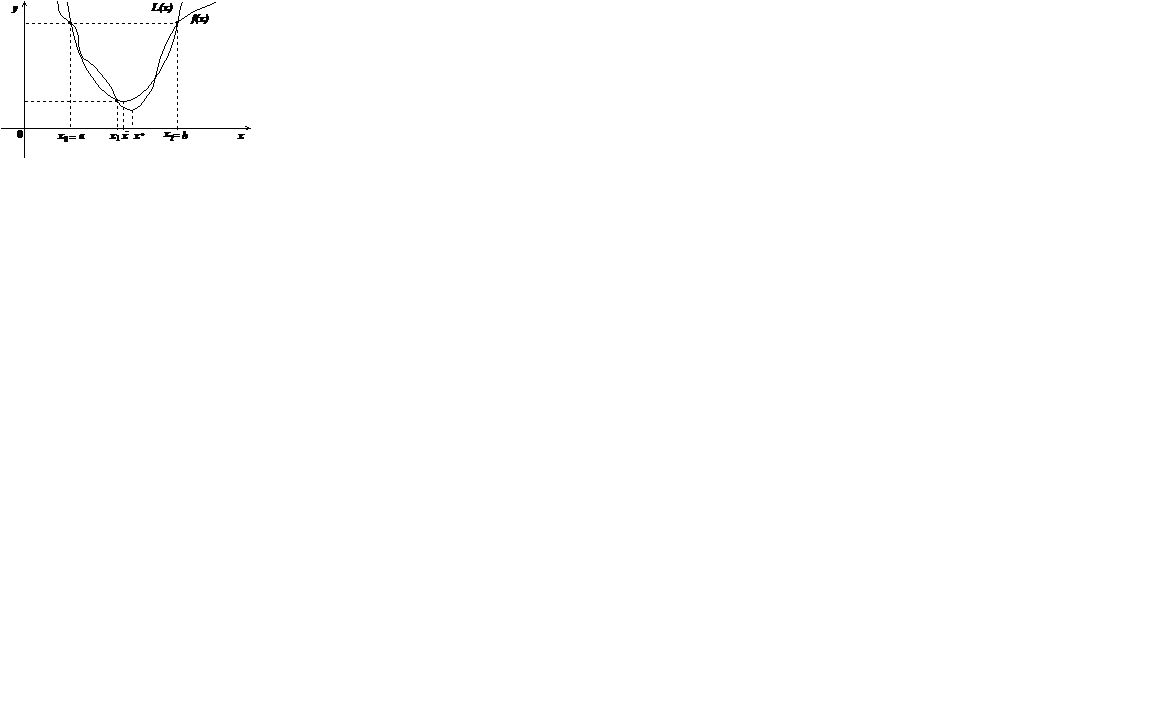
Рис. 11. Рис. 12.

Далі із точок треба вибрати нову вдалу трійку i повторити обчислення за формулою (20) і т.д.

Закінчити пошук наближеного значення точки мінімуму можна, якщо виконується умова i покласти при цьому , .

Метод парабол доцільно застосовувати після того, як знайдено відрізок локалізації мінімуму досить малої довжини. Наприклад, такий відрізок може бути отриманий після кроків методу дихотомії або золотого перерізу.

Чисельні експерименти показують, що якщо функція 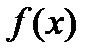добре апроксимується параболою в околі множини розв’язків , то цей метод виявляється більш ефективним, ніж інші методи мінімізації.

Розглянемо один з алгоритмів, який реалізує метод парабол.

Спочатку опишемо процедуру знаходження вдалої трійки для функції на відрізку локалізації точки мінімуму цієї функції.

Нехай задані точки такі, що , і відомі значення функції у цих точках: причому 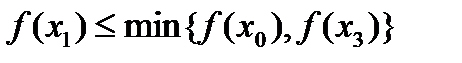i .

Якщо 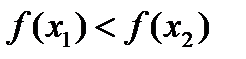, то покласти , , . Якщо , то покласти , , . Якщо , то i будь-яка трійка або буде вдалою. При цьому вибирають ту, якій відповідає менший з відрізків або .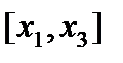

Дата добавления: 2015-08-21