Знаходження розв’язку задач методом динамічного програмування.

Розглянемо тепер в загальному вигляді розв’язок цієї задачі динамічного програмування. Для цього введемо деякі позначення і зробимо необхідні для подальшого викладення припущення.

Вважатимемо, що перебування даної системи на -му кроці () визначається сукупністю чисел 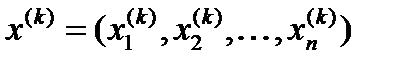, які отримані в результаті реалізації управління , що забезпечило перехід системи із стану в стан . При цьому передбачатимемо, що стан , в який перейшла система , залежить від даного стану і вибраного управління 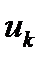і не залежить від того, яким чином система прийшла в стан .

Далі, вважатимемо, що якщо в результаті реалізації -го кроку забезпечений певний дохід або виграш, також залежний від початкового стану системи і вибраного управління і рівний , то спільний дохід або виграш за кроків складає

. (1)

Таким чином, ми сформулювали дві умови, якими повинна задовольняти дана задача динамічного програмування. Першу умову зазвичай називають умовою відсутності наслідків, а другу – умовою адитивності цільової функції задачі.

Виконання для задачі динамічного програмування першої умови дозволяє сформулювати для неї принцип оптимальності Беллмана. Перш ніж зробити це, дамо визначення оптимальної стратегії управління. Під такою стратегією розумітимемо сукупність управлінь , в результаті реалізації яких система за кроків переходить з початкового стану 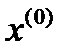в кінцевий і при цьому функція (1) набуває найбільшого значення.

Принцип оптимальності. Яким би не був стан системи перед черговим кроком, треба вибрати управління на цьому кроці так, щоб виграш на даному кроці плюс оптимальний виграш на всіх подальших кроках був максимальним.

Звідси витікає, що оптимальну стратегію управління можна отримати, якщо спочатку знайти оптимальну стратегію управління на -му кроці, потім на двох останніх кроках, потім на трьох останніх кроках і так далі, аж до першого кроку. Таким чином, розв’язок даної задачі динамічного програмування доцільно починати з визначення оптимального розв’язок на останньому, 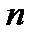-му кроці. Для того, щоб знайти цей розв’язок, очевидно, потрібно зробити різні припущення про те, як міг закінчитися передостанній крок, і з урахуванням цього вибрати управління , що забезпечує максимальне значення функції 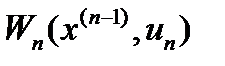. Таке управління , вибране при певних припущеннях про те, як закінчився попередній крок, називається умовно оптимальним управлінням. Отже, принцип оптимальності вимагає знаходити на кожному кроці умовне оптимальне управління для будь-якого з можливих результатів попереднього кроку.

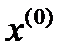Щоб це можна було здійснити практично, необхідно дати математичне формулювання принципу оптимальності. Для цього введемо деякі додаткові позначення. Позначимо через максимальний дохід, що отримується за кроків під час переходу системи з початкового стану в кінцевий стан при реалізації оптимальної стратегії управління 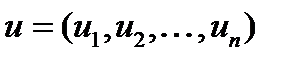, а через 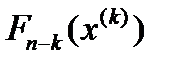– максимальний дохід, що отримується при переході з будь-якого стану в кінцевий стан при оптимальній стратегії управління на кроках, що залишилися. Тоді

. (2)

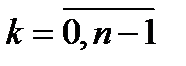, (). (3)

Останній вираз є математичним записом принципу оптимальності і носить назву основного функціонального рівняння Беллмана або рекурентного співвідношення. Використовуючи дане рівняння, знаходимо розв’язок даної задачі динамічного програмування. Зупинимося на цьому детальніше.

Вважаючи в рекурентному співвідношенні (3), отримуємо наступне функціональне рівняння:

,. (4)

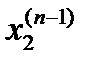У цьому рівнянні будемо вважати відомим. Використовуючи тепер рівняння (4) і розглядаючи всі допустимі стани системи на -му кроці , , … , …, знаходимо умовні оптимальні розв’язки

, , …, , …

і відповідні значення функції (4)

, , …, , …

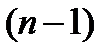Таким чином, на -му кроці знаходимо умовно оптимальне управління при будь-якому допустимому стані системи після -го кроку. Іншими словами, в якому б стані система не опинилася після -го кроку, нам вже відомо, яке слід прийняти рішення на -му кроці. Відомо також і відповідне значення функції (4).

Переходимо тепер до розгляду функціонального рівняння при :

,. (5)

Для того, щоб знайти значення для всіх допустимих значень , очевидно, необхідно знати і . Що стосується значень то ми їх вже визначили. Тому потрібно провести обчислення при деякому наборі допустимих значень і відповідних управлінь . Ці обчислення дозволять визначити умовно оптимальне управління для кожного . Кожне з таких управлінь спільно з вже вибраним управлінням на останньому кроці забезпечує максимальне значення доходу на двох останніх кроках.

Послідовно здійснюючи описаний вище ітераційний процес, дійдемо, нарешті, до першого кроку. На цьому кроці нам відомо, в якому стані може знаходитися система. Тому вже не потрібно робити припущень про допустимі стани системи, а залишається тільки вибрати управління, яке є найкращим з врахуванням умовних оптимальних управлінь, вже прийнятих на всіх подальших кроках.

Таким чином, в результаті послідовного проходження всіх етапів від кінця до початку визначаємо максимальне значення виграшу за кроків і для кожного з них знаходимо умовно оптимальне управління.

Щоб знайти оптимальну стратегію управління, тобто визначити шуканий розв’язок задачі, потрібно тепер пройти всю послідовність кроків, тільки цього разу від початку до кінця. А саме: на першому кроці в якості оптимального управління візьмемо знайдене умовне оптимальне управління . На другому кроці знайдемо стан , у який переводить систему управління . Цей стан визначає знайдене умовне оптимальне управління , яке тепер вважатимемо за оптимальне. Знаючи , знаходимо а значить, визначаємо і так далі. В результаті цього знаходимо розв’язок задачі, тобто максимально можливий дохід і оптимальну стратегію управління , що включає оптимальні управління на окремих кроках: .

Дата добавления: 2015-08-21