
|
Читайте также: |
(методу золотого перерізу )
Нехай задано  i відрізок
i відрізок  , на якому функція
, на якому функція  унімодальна.
унімодальна.
Крок 1. Знайти точки  і обчислити
і обчислити 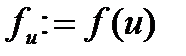 ,
,  .
.
Крок 2. Якщо  , то покласти
, то покласти 
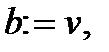
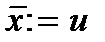 ,
,  ,
, 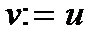 ,
,  , знайти
, знайти 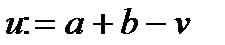 і обчислити
і обчислити 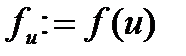 ;
;
інакше ( ) покласти
) покласти 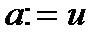 ,
, 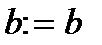 ,
, 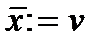 ,
, 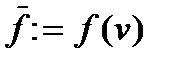 ,
, 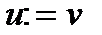 ,
,  , знайти
, знайти  і обчислити
і обчислити  .
.
Крок 3. Якщо  , то перейти на виконання кроку 4, інакше перейти до виконання кроку 2.
, то перейти на виконання кроку 4, інакше перейти до виконання кроку 2.
Крок 4. Вивести 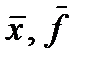 . Кінець алгоритму.
. Кінець алгоритму.
Зауваження. На жаль чисельна реалізація описаного алгоритму, а отже і методу золотого перерізу, призводить до того, що він стає практично незастосовним навіть при невеликих 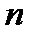 . Це викликано тим, що значення
. Це викликано тим, що значення 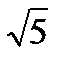 в ЕОМ обчислюється наближено і вже перші точки ітераційного процесу (див.(27.6)) будуть знайдені з деякою похибкою, яка при збільшенні
в ЕОМ обчислюється наближено і вже перші точки ітераційного процесу (див.(27.6)) будуть знайдені з деякою похибкою, яка при збільшенні 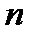 досить швидко накопичується, а це призводить до того, що порушується властивість симетричності методу.
досить швидко накопичується, а це призводить до того, що порушується властивість симетричності методу.
Розглянемо модифікований алгоритм методу золотого перерізу, який у випадку порушення симетричності методу, а, точніше, коли на деякому кроці 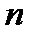 буде
буде  , перераховує для поточного відрізка
, перераховує для поточного відрізка  золотий переріз за формулами (27.6), що забезпечує його практичну застосовність до розв’язування задач одновимірної мінімізації та перевагу перед методом дихотомії за кількістю обчислень значень функції
золотий переріз за формулами (27.6), що забезпечує його практичну застосовність до розв’язування задач одновимірної мінімізації та перевагу перед методом дихотомії за кількістю обчислень значень функції  при заданій точності
при заданій точності  .
.
Дата добавления: 2015-08-21; просмотров: 140 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод золотого перерізу | | | Метод Фібоначчі. |