
Читайте также:
|
Розглянемо метод мінімізації унімодальної функції на заданому відрізку, який за своєю структурою є досить простим і дозволяє розв'язати задачу з необхідною точністю при меншій кількості обчислень значень функції порівняно з методом дихотомії.
В основу цього методу покладено властивості золотого перерізу відрізка.
Поділ відрізка на дві нерівні частини так, що відношення довжини всього відрізка до довжини його більшої частини дорівнює відношенню довжини більшої частини до довжини меншої частини відрізка називається золотим перерізом цього відрізка.
Визначимо точки, якi здійснюють золотий переріз заданого відрізка  .
.
Очевидно, що таких точок буде дві (рис. 7. а).


a) б)
Рис. 7.
Згідно означення золотого перерізу, можна скласти два рівняння відносно невідомих  i
i  відповідно:
відповідно:
 (5)
(5)
 (6)
(6)
Розв'язок рівнянь (5) i (6) будемо шукати у вигляді:
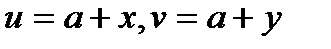 ,
,
де 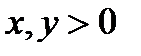 і
і  (рис. 7. б).
(рис. 7. б).
Одержуємо два квадратних рівняння
 ,
,
 ,
,
коренями яких є
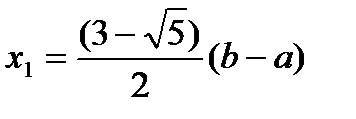 і
і  ,
,
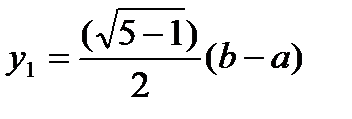 і
і  .
.
Оскільки для точок 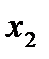 i
i 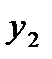
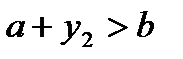 i, то золоті перерізи визначаються точками
i, то золоті перерізи визначаються точками
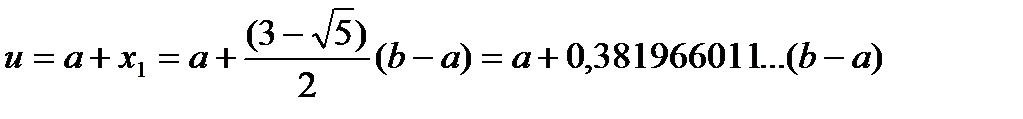 , (7)
, (7)
 . (8)
. (8)
Ці точки розташовані симетрично відносно середини відрізка  i
i 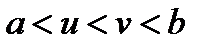 , при цьому шукане відношення між довжинами відрізків у золотому перерізі, наприклад, з (5) і (7) дорівнює
, при цьому шукане відношення між довжинами відрізків у золотому перерізі, наприклад, з (5) і (7) дорівнює
 . (9)
. (9)
Точка u називається першою точкою золотого перерізу, а точка v – другою.
Зауважимо, що точка  є, в свою чергу, другою точкою золотого перерізу відрізка
є, в свою чергу, другою точкою золотого перерізу відрізка  . Дійсно, із означення золотого перерізу i формул (7), (8) маємо нерівність
. Дійсно, із означення золотого перерізу i формул (7), (8) маємо нерівність 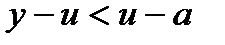 і рівність
і рівність  . Тоді, враховуючи (9),
. Тоді, враховуючи (9),
 тобто
тобто 
Аналогічно можна показати, що точка  є першою точкою золотого перерізу відрізка
є першою точкою золотого перерізу відрізка  .
.
Знаючи одну з точок золотого перерізу відрізка  , іншу можна знайти за однією з формул:
, іншу можна знайти за однією з формул:
 або
або  .
.
Використовуючи розглянуті властивості золотого перерізу, можна запропонувати такий метод мінімізації унімодальної на відрізку  функції
функції  .
.
Нехай  – задана точність відшукання точки мінімуму. Покладемо на першому кроці
– задана точність відшукання точки мінімуму. Покладемо на першому кроці  , знайдемо точки
, знайдемо точки  i
i  , наприклад, за формулами
, наприклад, за формулами
 (10)
(10)
i обчислимо значення функції  у цих точках:
у цих точках:  .
.
Якщо  (рис. 8 а)), то покласти
(рис. 8 а)), то покласти  ,
, 
 ,
,  , знайти
, знайти 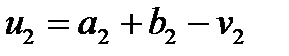 i обчислити
i обчислити  .
.


а) б)
Рис. 8.
Якщо  (рис 8 б)), то покласти
(рис 8 б)), то покласти  ,
, 
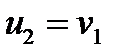 ,
,  , знайти
, знайти  i обчислити
i обчислити  .
.
В силу унімодальності функції  на
на  , відрізок
, відрізок  має хоча б одну спільну точку з множиною
має хоча б одну спільну точку з множиною 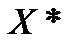 точок мінімуму
точок мінімуму  на
на  . При цьому довжина відрізка
. При цьому довжина відрізка  дорівнює
дорівнює
 (11)
(11)
Дійсно, при 
 ,
,  і тоді
і тоді
 ,
,
а при 
 ,
,  і тоді
і тоді

Нехай вже визначений відрізок  , знайдені точки
, знайдені точки  , значення
, значення  ,
,  , при цьому, в загальному випадку,
, при цьому, в загальному випадку,  і
і
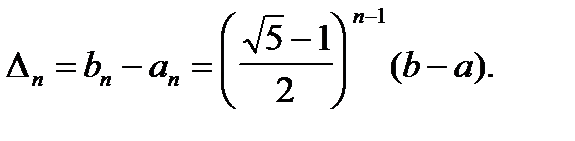 (12)
(12)
Якщо  , то процес обчислень закінчується, i за наближений розв'язок задачі можна взяти точку
, то процес обчислень закінчується, i за наближений розв'язок задачі можна взяти точку  , якщо
, якщо  , або
, або  , якщо
, якщо  , при цьому похибка наближення
, при цьому похибка наближення  , з урахуванням (27.7), не перевищує величину
, з урахуванням (27.7), не перевищує величину

 . (13)
. (13)
Якщо ж  то при
то при  покласти
покласти  ,
,  ,
,  ,
,  , знайти
, знайти  і обчислити
і обчислити  , інакше покласти
, інакше покласти  ,
, 
 ,
,  , знайти
, знайти  i обчислити
i обчислити  .
.
Після чого треба повторити перевірку умови  i т.д.
i т.д.
Як видно з опису методу, на кожному його кроці (крім першого) обчислюється лише одне значення функції  (на відміну від методу дихотомії). Кількість кроків
(на відміну від методу дихотомії). Кількість кроків 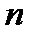 методу золотого перерізу, яка забезпечує задану точність знаходження наближення до деякої точки
методу золотого перерізу, яка забезпечує задану точність знаходження наближення до деякої точки  , задовольняє нерівність (див. (13))
, задовольняє нерівність (див. (13))
 .
.
Розглянемо алгоритм, який реалізує описаний метод золотого перерізу.
Дата добавления: 2015-08-21; просмотров: 127 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Алгоритм 2. | | | Алгоритм 3 |