Метод дихотомії

Найпростішим наближеним методом, який використовує лише інформацію про значення цільової функції в точках допустимої множини є метод поділу відрізка навпіл (або метод дихотомії).

Нехай функція унімодальна на відрізку .

У процесі роботи методу дихотомії будується послідовність вкладених відрізків

,

кожен з яких містить хоча б одну точку мінімуму функції на .

Нехай задані числа (необхідна точність визначення точки ) і .

Пошук точки мінімуму функції на відрізку починається з вибору двох точок 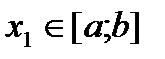, за правилом:

, .

Точки розміщені симетрично відносно середини відрізка і при малих ділять відрізок майже навпіл (звідси назва методу).

Перехід від відрізка до відрізка відбувається так:

якщо , то покладають (рис. 5 а), в протилежному випадку (рис. 5 б).

а) б)

Рис. 5.

В силу унімодальності функції на відрізку зрозуміло, що відрізок має хоча б одну спільну точку з множиною точок мінімуму функції на (рис. 5, 6) і його довжина дорівнює

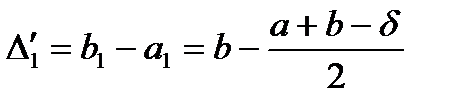або і

Для зручності подальших обрахунків для визначення будемо використовувати співвідношення

. (2)

Рис. 6.

Нехай вже отриманий відрізок такий, що 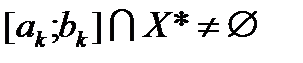, при цьому, з урахуванням (2), його довжина дорівнює

.

Отже,

. (3)

Якщо , то задача розв'язана із заданою точністю і за наближення до деякої точки 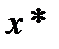множини можна взяти точку , якщо , або , якщо 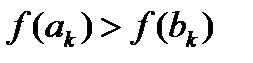, а значення буде наближенням для .

Зауваження. На практиці часто за наближення точки мінімуму функції на 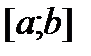приймають точку з меншою ніж в попередньому випадку похибкою:

.

Якщо ж величина , то визначаються точки

, .

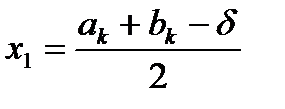і обчислюються значення 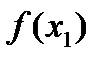і .

Якщо , то покладають 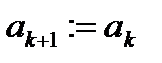, , інакше , .

Згідно з (3), довжина отриманого відрізка дорівнює

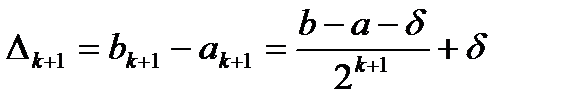
і . Після чого повторюється перевірка умови 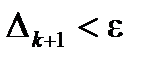і т.д.

Розглянемо алгоритм, який реалізує описаний метод дихотомії і, також, визначає кількість зроблених ітерацій для досягненні точності і кількість обчислень значень цільової функції . Параметри і на практиці використовуються для контролю кількості можливих обчислень значень функції, а також для порівняння з іншими методами.

Дата добавления: 2015-08-21