Алгоритм 1

(пошуку відрізка локалізації точки мінімуму)

Нехай задані довільне початкове наближення , і величина кроку .

Крок 0. Покласти і обчислити .

Крок 1. Якщо то покласти , і перейти до виконання кроку 5.

Крок 2. Покласти і обчислити .

Крок 3. Якщо то покласти , , і перейти до виконання кроку 5.

Крок 4. Покласти і перейти до виконання кроку 0.

Крок 5. Покласти і обчислити .

Крок 6. Якщо , то покласти , , , і перейти до виконання кроку 5.

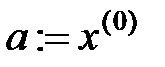Крок7. Якщо , то покласти , , , інакше покласти , , , .

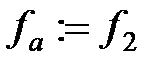Кінець алгоритму.

Зауваження:

1.Трійка чисел , яка одержується в результаті роботи алгоритму, є вдалою трійкою і використовується в деяких методах одновимірної мінімізації, зокрема в методі парабол.

2. Якщо початкове наближення знаходиться в - околі точки мінімуму функції (де - досить мале додатне число), то алгоритм 2 можна застосовувати безпосередньо для знаходження наближеного значення з точністю до . Для цього до алгоритму 2 треба ввести ще один параметр - точність наближеного розв'язку і після кроку 7 добавити ще один крок:

Крок 8. Якщо 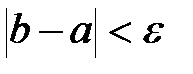, то покласти , і кінець алгоритму, інакше вивести .

3. Алгоритм 1 погано працює у випадку коли (операція і повернення на крок 0 продовжується доти, поки ЕОМ буде розрізняти значення i ). Щоб запобігти цьому, крок 4 алгоритму 2 можна замінити на такий:

Крок 4. Якщо , то покласти , і кінець алгоритму, інакше покласти і перейти на крок 0.

Дата добавления: 2015-08-21