Метод Фібоначчі.

У тих випадках, коли обчислення значень функції пов'язане з певними труднощами, важливого значення набувають найбільш економічні методи, які дозволяють розв'язати задачу мінімізації з потрібною точністю при якомога меншій кількості обчислень значень функції, що мінімізується. Розглянемо один з таких методів, який є оптимальним, для класу унімодальних функцій i тісно пов'язаний із числами Фібоначчі.

Як відомо, числа Фібоначчі визначаються співвідношеннями:

(14)

Наведемо кілька перших чисел Фібоначчі:

, , , , , , , , , , , , ,…, ,…,

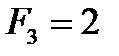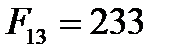За методом індукції можна довести, що - те число Фібоначчі можна подати у вигляді:

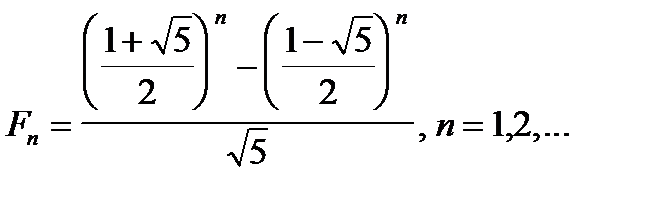– формула Біне.

Звідси випливає, що при досить великому

(15)

тобто числа Фібоначчі із зростанням зростають досить швидко.

Нехай – унімодальна на відрізку функція i задано число 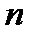обчислень значень цієї функції, яке повинно забезпечити необхідну точність відшукання наближення деякої точки мінімуму на .

Метод Фібоначчі, як i метод золотого перерізу, відноситься до класу симетричних методів i визначається заданням на відрізку двох точок, симетричних відносно його середини (рис. 9):

і .

Рис. 9.

Далі на кожному кроці методу точка чергового обчислення вибирається симетрично відносно середини поточного відрізка локалізації до точки, яка лежить внутрі цього відрізка і знайдена на попередньому кроці.

Розглянемо перші кроки методу Фібоначчі. Нехай , . Знайдемо 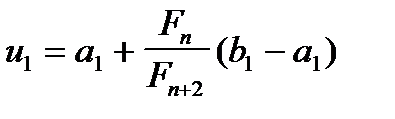, , 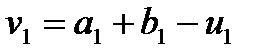де , 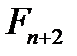– відповідні числа Фібоначчі при заданому 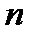, які знаходяться за допомогою рекурентного співвідношення (14) або за формулою Біне.

Якщо , то наступним відрізком локалізації є відрізок , де , . У цьому випадку точка буде визначати точку 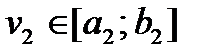, тобто , а точка 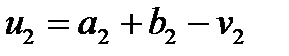. Крім того, можна легко перевірити, що .

Якщо ж , то наступним відрізком локалізації є відрізок , де , . У цьому випадку точка буде визначати точку 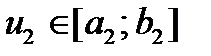, тобто 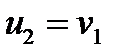, а точка . Крім того, можна легко перевірити, що .

За методом індукції можна показати, що на -му кроці методу Фібоначчі буде отримана трійка , яка локалізує хоча б одну точку з множини 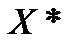точок мінімуму функції 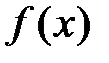i така, що

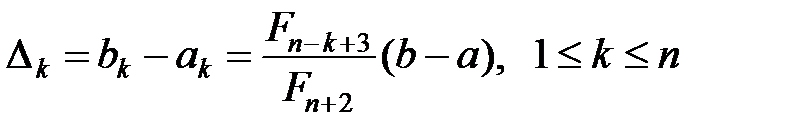, (16)

, а точка , для якої ,

співпадає з однією з точок

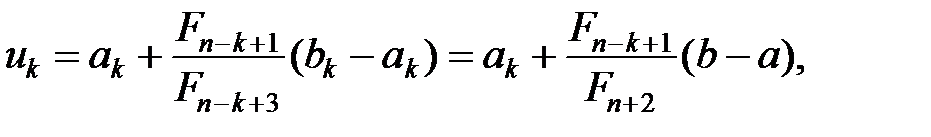(17)

які розташовані на відрізку симетрично відносно його середини. При процес закінчується. В цьому випадку згідно формул (14), (16), (17) довжина відрізка дорівнює

, (18)

а точки

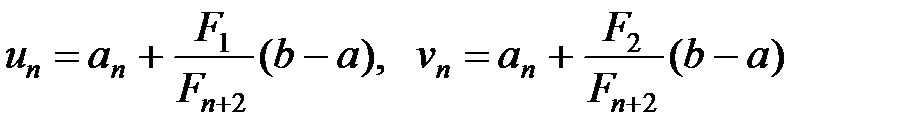
співпадають (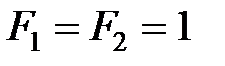) і є серединою відрізка .

За наближений розв'язок задачі пошуку мінімуму функції 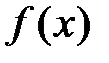на проміжку приймають величину , де . При цьому похибка наближення , з урахуванням (18), не перевищує величину

.

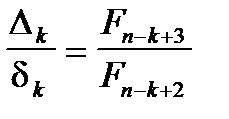Зауваження. Після кроків методу Фібоначчі відношення довжини відрізка локалізації (див. (28.3)) до довжини більшого відрізка (див. (17)), дорівнює . Тоді, враховуючи (15), при досить великих 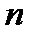маємо

.

Крім того, , , тобто при досить великому 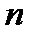початкові точки методів Фібоначчі та золотого перерізу практично співпадають.

Це зауваження свідчить про тісний зв’язок між методами Фібоначчі та золотого перерізу.

Розглянемо алгоритм, який реалізує метод Фібоначчі.

Дата добавления: 2015-08-21