Зауваження.

1. Числа Фібоначчі , 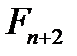при заданому 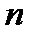на кроці 1 алгоритму 5 знаходяться за допомогою рекурентного співвідношення (14) або за формулою Біне.

2. При практичній реалізації описаного алгоритму, а отже і методу Фібоначчі, треба мати на увазі, що число , взагалі кажучи, є нескінченним періодичним дробом, тому перша точка буде знайдена наближено. В зв’язку з цим похибка у визначенні цієї точки, як правило, призводить до швидкого зростання похибки на наступних ітераціях методу, і вже при не дуже великих 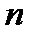симетричність методу порушується.

Розглянемо модифікований алгоритм 5, який у випадку порушення симетричності методу, а, точніше, коли на деякому кроці буде , обчислює для поточного відрізка точку за рекурентним співвідношенням (17), а точку за формулою , що забезпечує його практичну застосовність до розв’язування задач одновимірної мінімізації.

Дата добавления: 2015-08-21