
|
Читайте также: |
Раздел 1. Интегральное исчисление
1)Первообразная функции и ее связь с неопределенным интегралом. Таблицы интегралов. Замена переменной в неопределенном интеграле.
2)Интегрирование по частям. Интегрирование простейших дробей.
3)Интегрирование простейших иррациональностей.
4)Интегрирование рациональностей, зависящих от простейших тригонометрических функций.
5)Интегральная сумма. Определение определенного интеграла и его геометрический смысл. Свойства определенного интеграла. Теорема о среднем. Формула Ньютона–Лейбница.
6)Площадь криволинейной трапеции и криволинейного сектора.
7)Длина дуги кривой. Объем тела вращения вокруг оси ОХ.
8)Несобственные интегралы.
9)Двойной интеграл, выражение его через повторный интеграл. Геометрический и механический смысл двойного интеграла.
10)Криволинейные интегралы. Формула Грина.
11)Приближенное вычисление интегралов.
Раздел 2. Дифференциальные уравнения
12)Понятие дифференциального уравнения (ДУ) и его порядка. Понятие общего и частного решений. ДУ с разделяющимися переменными.
13)ДУ 1-го порядка в однородных функциях. Линейные ДУ первого порядка. Уравнение Бернулли. Понижение порядка ДУ.
14)Линейные ДУ 2-го порядка с постоянными коэффициентами.Метод вариации произвольных постоянных решения ДУ.
15)Численные методы решения ДУ.
Раздел 3. Ряды и гармонический анализ
16) Числовой ряд, его сходимость и сумма. Необходимый признак сходимости. Свойства сходящихся рядов. Геометрический и обобщенный гармонический ряды.
17) Признаки сходимости положительных рядов: сравнения, Даламбера, радикальный и интегральный признаки Коши.
18) Знакопеременные ряды, абсолютная и условная сходимость. Признак Лейбница.
19) Степенные ряды. Область сходимости.
20) Ряды Фурье.
1) Первообразная функции и ее связь с неопределенным интегралом. Таблицы интегралов. Замена переменной в неопределенном интеграле.
Понятие первообразной и неопределенного интеграла.
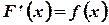
Функция  называется первообразной функцией для функции
называется первообразной функцией для функции 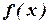 на интервале
на интервале 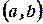 , если
, если  дифференцируема на интервале
дифференцируема на интервале 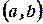 и
и 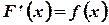 .
.
Аналогично можно определить понятие первообразной и на отрезке 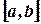 , но в точках
, но в точках  и
и 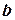 надо рассматривать односторонние производные.
надо рассматривать односторонние производные.
Теорема. Если  первообразная для функции
первообразная для функции 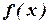 на
на 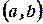 , то
, то 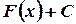 - также первообразная, где
- также первообразная, где 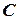 - любое постоянное число.
- любое постоянное число. 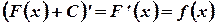 .
.
Определение. Произвольная первообразная для 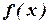 на
на 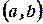 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 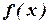 и обозначается символом
и обозначается символом 
Знак  называется интегралом,
называется интегралом,  - подынтегральное выражение,
- подынтегральное выражение, 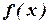 - подынтегральная функция.
- подынтегральная функция.
Таким образом, если  одна из первообразных для
одна из первообразных для 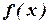 , то
, то 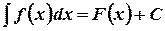
Операцию нахождения неопределенного интеграла называют интегрированием функции 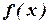 . Она противоположна операции дифференцирования.
. Она противоположна операции дифференцирования.
2. Свойства неопределённых интегралов.
1. 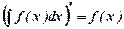 2.
2. 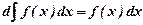
3. 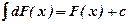 4.
4. 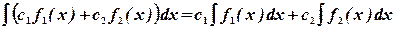
3. Таблица основных неопределенных интегралов.
1. 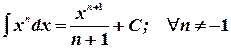


2. 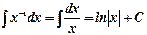
3. 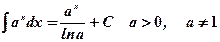 ;
; 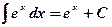
4. 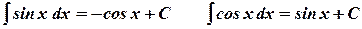
5. 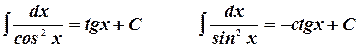
6. 
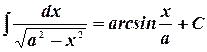
7. 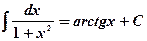

8. 


9. 
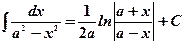
10. 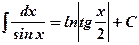
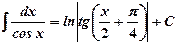
Отметим, что операция дифференцирования элементарных функций снова приводит к элементарным функциям. Операция интегрирования уже может привести к неэлементарным функциям, т.е. функциям, которые не выражаются через конечное число арифметических операций и суперпозицией элементарных функций.
Например, доказано, что следующие интегралы не интегрируются в элементарных функциях.
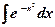 - интеграл Пуассона.
- интеграл Пуассона.
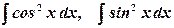 - интегралы Френеля.
- интегралы Френеля.
 - интегральный логарифм.
- интегральный логарифм.
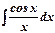 - интегральный косинус.
- интегральный косинус.
 - интегральный синус.
- интегральный синус.
Дата добавления: 2015-08-21; просмотров: 166 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Закольцованный ролик | | | Метод интегрирования подстановкой |