Интегрирование иррациональных выражений.

1. Интегралы вида Пусть – общий знаменатель . Тогда эффективна замена переменных:

2. Интегралы вида Пусть – общий знаменатель . Тогда эффективна замена .

Интегрирование рациональных функций, т.е интегрирование выражений вида:

В зависимости от конкретного вида выражения, существуют разные способы интегрирования.

1. Выделение полного квадрата

2. Тригонометрические замены.

4) Интегрирование рациональностей, зависящих от простейших тригонометрических функций.

Для нахождения интегралов вида , где - рациональная функция, используют универсальную тригонометрическую подстановку .

Тогда

.

То есть подынтегральная функция приобретает вид:

Например, возьмем интеграл . Для этого введем новую переменную . Тогда, как было показано выше и 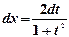. Подставим эти значения в искомый интеграл:

Частные случаи.

1. Интегралы вида

При этом делаем замену . Тогда

2. Интегралы вида , где и натуральные числа.

Данные интегралы находятся с помощью тригонометрических формул , , , если и – четные.

Если хотя бы одно из чисел и - нечетное, то от нечетной степени отделяется множитель и вводится новая переменная:

если интеграл имеет вид , то замена переменных: .

Если интеграл имеет вид то замена переменных: .

Используя тригонометрическое тождество

можно упростить взятие некоторых интегралов.

Например:

5) Интегральная сумма. Определение определенного интеграла и его геометрический смысл.

---

Дата добавления: 2015-08-21