Формула Ньютона-Лейбница

Вычисление определенного интеграла как предела интегральной суммы очень сложно.

Ньютон и Лейбниц доказали теорему, связывающую два важных понятия математического анализа - интеграла и производной. Эта теорема выражается соотношением ( формула Ньютона-Лейбница )

Таким образом, для того чтобы вычислить определенный интеграл от непрерывной функции на отрезке 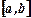, надо найти ее первообразную функцию 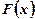и взять разность значений этой первообразной на концах отрезка .

Еще раз отметим, что определенный интеграл это число, в то время как неопределенный - это функция. Поэтому совершенно все равно, по какой переменной (букве) ведется интегрирование

Например, вычислить интеграл 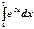. Имеем

6)Площадь криволинейной трапеции и криволинейного сектора.

а) Площадь криволинейной трапеции ( явное задание функции ).

Зададим на отрезке 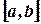( и 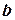- конечные числа) неотрицательную, непрерывную функцию , график которой изображен на рисунке.

Произведем разбиение отрезк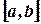а на - частей точками

Выберем на каждом из полученных частичных отрезков () по произвольной точке . Определим значения функции в этих точках и составим сумму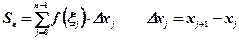

которую называют интегральной суммой и которая, очевидно, равна сумме площадей заштрихованных прямоугольников, как показано на рисунке.

Предел, к которому стремится интегральная сумма, когда называется определенным интегралом от функции на отрезке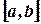

Если функция отрицательна внутри отрезка 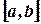, то интеграл по абсолютному значению равен площади, покрываемой графиком, но имеет отрицательное значение (см. рис.).

Пусть теперь меняет знак на интервале 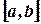, как показано на рисунке.

В этом случае определенный интеграл будет подсчитываться как

в) Площадь криволинейного сектора ( кривая в полярных координатах ) дается формулой

Действительно, согласно рисунку, площадь элементарного сектора представляет собой площадь треугольника, равную половине произведения основания на высоту

Отсюда вытекает основная формула.
7)Длина дуги кривой. Объем тела вращения вокруг оси ОХ.

8. Вычисление длины дуги плоской кривой.

Длинна кривой линии – это предел длины вписанной в нее ломанной, когда длина наибольшего звена стремится к нулю. Если этот предел существует, то кривая называется спрямляемой.

Теорема. Пусть дана непрерывная, дифференцируемая на 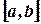функция 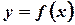. Следовательно, ее производная тоже непрерывна, причем . Тогда длина дуги графика функции определяется выражением

Доказательство. Согласно рисунку, . Отсюда длина элементарной дуги будет равна . Длина всей дуги будет равна

Кривая задана параметрически.

В этом случае . Тогда . Следовательно

И, соответственно

9. Вычисление объёма тела по площади поперечного сечения.

Пусть нам дано тело, известные площади поперечного сечения 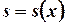которого расположены перпендикулярно оси , как показано на рисунке. Тогда элементарный объем этого тела будет равен

Соответственно полный объем этого тела будет выражаться формулой

Вычисление объем тела вращения.

Формула для объема получается из предыдущей, где .

8)Несобственные интегралы.

Пусть на конечном полуинтервале задана функция такая, что она интегрируема (т.е. конечна) на любом интервале , где , но неограниченна в окрестности точки 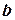. Тогда ее интеграл на , или, что то же самое, на 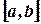не может существовать, так как интегрируемая функция должна быть ограничена.

Однако может случиться так, что существует конечный предел

То есть функция не ограничена, а ее интеграл ограничен. В этом случае записанный предел называют несобственным интегралом от на отрезке 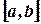и записывают в виде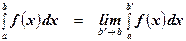

В таком случае говорят, что интеграл сходится. В противном случае говорят, что он расходится или не существует как несобственный риманов интеграл.

Аналогично и на полуинтервале

В связи с этим выражение

называется интегралом от с единственной особенностью в точке 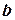, если выполняется следующее условие: если 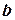конечная точка, то функция интегрируема на при любом удовлетворяющим неравенствам , и, кроме того, не ограничена в точке 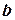. Если же , то про функцию предполагается лишь, что она интегрируема на при любом конечном .

Также различают несобственные интегралы первого типа (с одним или двумя бесконечными пределами) и несобственные интегралы второго типа (от разрывных функций).

Несобственный интеграл первого рода, вычисляется обычно как

Например, найти . Имеем .

При 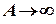это выражение имеет предел . Значит.

Или, найти . Имеем . Этот интеграл расходится.

13)ДУ 1-го порядка в однородных функциях. Линейные ДУ первого порядка. Уравнение Бернулли. Понижение порядка ДУ.

Дата добавления: 2015-08-21