Положительные ряды.

Для исследования сходимости положительных рядов (т.е. рядов с неотрицательными членами: ³0)применяют достаточные признаки сходимости рядов.

Пример 4. Исследовать сходимость ряда

Решение. Применим признак Даламбера. Записываем n- ый член ряда: (n +1 )- ый член получим, если в выражении везде n заменим на (n+ 1 ): Найдем предел отношения:

Пример 2.Исследовать сходимость ряда Решение. Применим первый признак сравнения. В качестве «эталонного» ряда возьмем обобщенный гармонический ряд	Показатель степени гармонического ряда p =4/5<1, поэтому «эталонный» ряд расходящийся. Члены исходного ряда для всех n³3 превосходят соответствующие члены «эталонного» ряда: Применяя первый признак сравнения, получаем, поскольку расходится «меньший» эталонный ряд, то расходится и «больший» исходный ряд.
Пример 3. Исследовать сходимость ряда Решение. Преобразуем общий член исходного ряда	Исходный ряд сравним с “эталонным” рядом Это “ геометрический ряд, он сходится, т.к. знаменатель прогрессии q =2/3<1. Поскольку - конечное число, отличное от 0, то в силу второго признака сравнения заключаем, что исходный ряд сходится.
Пример 5. Исследовать сходимость ряда Решение.Здесь удобно применить радикальный признак Коши:	Следовательно, ряд сходится. Подчеркнем, здесь использовали известный «второй замечательный» предел
Пример 6. Исследовать сходимость ряда Решение.Рассмотрим функцию 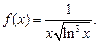Она при x³2 положительная, непрерывная и монотонно убывает. Можно применять интегральный признак.	Исследуем сходимость несобственного интеграла: Из интегрального признака заключаем, поскольку несобственный интеграл сходится, то сходится и исследуемый ряд.

18) Знакопеременные ряды, абсолютная и условная сходимость. Признак Лейбница.

Дата добавления: 2015-08-21