Метод интегрирования подстановкой

Основную роль в интегральном исчислении играет формула замены переменных (или подстановки )

Пример. .

Такого табличного интеграла нет. Сделаем замену - . Отсюда

2) Интегрирование по частям. Интегрирование простейших дробей.

6. Интегрирование по частям.

Известно, что дифференциал от произведения равен:

Проинтегрируем полученное равенство

Интеграл от дифференциала некоторой функции равен самой функции:

Меняя местами слагаемые, получим:

Это и есть формула интегрирования по частям.

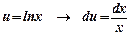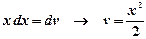Пример. Вычислить интеграл . Решение. Положим ; . Тогда

7. Интегрирование рациональных дробей.

Дробью называется выражение вида:

Дробь - правильная, если . Дробь - не правильная, если .

Для того, чтобы проинтегрировать дробь надо разложить ее на простейшие Простейшие дроби:

1. 2. 3.

4.

Интеграл от 1 дроби-табличный интеграл: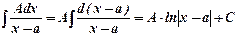

Интеграл от 2 дроби - также табличный:

3. Интеграл от третьей дроби см. интеграл группы четырёх.

4. Интеграл от четвертой дроби также см. интеграл группы четырёх.

Таким образом, дроби общего вида сводятся к простейшим дробям.

3)Интегрирование простейших иррациональностей.

Дата добавления: 2015-08-21